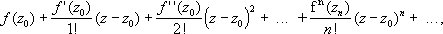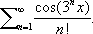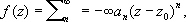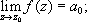|
|
Популярные авторы:: Эллисон Харлан :: Ломер Кит :: Говард Роберт Ирвин :: Лем Станислав :: Желязны Роджер :: Лавкрафт Говард Филлипс :: Ламур Луис :: Шукшин Василий Макарович :: Лесков Николай Семёнович :: Азимов Айзек Популярные книги:: Снежная страна :: Справочник по реестру Windows XP :: Бурый волк :: Лопатка :: Последний коммунист :: Дунайский лоцман :: Вирусы мозга :: Шотландский лев :: Дом страха :: Автобан нах Познань |
Большая Советская Энциклопедия (АН)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (АН) - Чтение (стр. 5)
В период иатрохимии (16-17 вв.) ещё более увеличился удельный вес химических методов исследования, особенно методов «мокрого» качественного исследования веществ, переводимых в растворы: так, серебро и соляная кислота распознавались по реакции образования ими осадка в азотнокислой среде; пользовались реакциями с образованием окрашенных продуктов, например железа с дубильными веществами. Начало научному подходу к химическому анализу положил английский учёный Р. Бойль (17 в.), когда он, отделив химию от алхимии и медицины и став на почву химического атомизма, ввёл понятие химического элемента как неразложимой далее составной части различных веществ. Согласно Бойлю, предметом химии является изучение этих элементов и способов их соединения для образования химических соединений и смесей. Разложение веществ на элементы Бойль и назвал «анализом». Весь период алхимии и иатрохимии был в значительной степени периодом синтетической химии; были получены многие неорганические и некоторые органические соединения. Но т. к. синтез был тесно связан с анализом, ведущим направлением развития химии в это время был именно анализ. Новые вещества получались в процессе всё более утончённого разложения природных продуктов. Т. о., почти до середины 19 в. химия развивалась преимущественно как А. х.; усилия химиков были направлены на разработку методов определения качественно различных начал (элементов), на установление количественных законов их взаимодействия. Большое значение в химическом анализе имела дифференциация газов, считавшихся ранее одним веществом; начало этим исследованиям было положено голландским учёным ван Гельмонтом (17 в.), открывшим углекислый газ. Наибольших успехов в этих исследованиях достигли Дж. Пристли, К. В. Шееле, А. Л. Лавуазье (18 в.). Экспериментальная химия получила твёрдую основу в установленном Лавуазье законе сохранения массы веществ при химических операциях (1789). Правда, ещё ранее этот закон в более общей форме высказал М. В. Ломоносов (1758), а шведский учёный Т. А. Бергман пользовался сохранением массы веществ для целей химического анализа. Именно Бергману принадлежит заслуга создания систематического хода качественного анализа, при котором переведённые в растворённое состояние исследуемые вещества затем разделяются на группы с помощью реакций осаждения реагентами и далее дробятся на ещё меньшие группы вплоть до возможности определения каждого элемента в отдельности. В качестве основных групповых реактивов Бергман предложил сероводород и щёлочи, которыми пользуются и до сих пор. Он также систематизировал качественный анализ «сухим путём», посредством нагревания веществ, которое приводит к образованию «перлов» и налётов различного цвета. Дальнейшее совершенствование систематического качественного анализа было выполнено французскими химиками Л. Вокленом и Л. Ж. Тенаром, немецкими химиками Г. Розе и К. Р. Фрезениусом, русским химиком Н. А. Меншуткиным. В 20-30-е гг. 20 в. советский химик Н. А. Тананаев, основываясь на значительно расширившемся наборе химических реакций, предложил дробный метод качественного анализа, при котором отпадает необходимость систематического хода анализа, разделения на группы и применения сероводорода. Количественный анализ первоначально основывался на реакциях осаждения определяемых элементов в виде малорастворимых соединений, массу которых далее взвешивали. Этот весовой (или гравиметрический) метод анализа также значительно усовершенствовался со времён Бергмана, главным образом за счёт улучшения весов и техники взвешивания и использования различных реактивов, в частности органических, образующих наименее растворимые соединения. В 1-й четверти 19 в. французский учёный Ж. Л. Гей-Люссак предложил объёмный метод количественного анализа (волюмометрический), в котором вместо взвешивания измеряют объёмы растворов взаимодействующих веществ. Этот метод, называемый также методом титрования или титриметрическим, до сих пор является основным методом количественного анализа. Он значительно расширился как за счёт увеличения числа используемых в нём химических реакций (реакции осаждения, нейтрализации, комплексообразования, окисления-восстановления), так и за счёт использования множества индикаторов (веществ, указывающих изменениями своего цвета на окончание реакции между взаимодействующими растворами) и др. средств индикации (посредством определения различных физических свойств растворов, например электропроводности или коэффициента преломления). Анализ органических веществ, содержащих в качестве основных элементов углерод и водород, посредством сожжения и определения продуктов сгорания - углекислого газа и воды - впервые был проведён Лавуазье. Далее он был улучшен Ж. Л. Гей-Люссаком и Л. Ж. Тенаром и Ю. Либихом. В 1911 австрийский химик Ф. Прегль разработал технику микроанализа органических соединений, для проведения которого достаточно нескольких мгисходного вещества. Ввиду сложного построения молекул органических веществ, больших их размеров (полимеры), ярко выраженной изомерии органический анализ включает в себя не только элементный анализ - определение относительных количеств отдельных элементов в молекуле, но и функциональный - определение природы и количества отдельных характерных атомных группировок в молекуле. Функциональный анализ основан на характерных химических реакциях и физических свойствах изучаемых соединений. Почти до середины 20 в. анализ органических веществ, в силу своей специфичности, развивался своими, отличными от неорганического анализа путями и в учебных курсах не включался в А. х. Анализ органических веществ рассматривался как часть органической химии. Но затем, по мере возникновения новых, главным образом физических, методов анализа, широкого применения органических реактивов в неорганическом анализе обе эти ветви А. х. стали сближаться и ныне представляют единую общую научную и учебную дисциплину. А. х. как наука включает теорию химических реакций и химических свойств веществ и как таковая она в первый период развития общей химии совпадала с ней. Однако во 2-й половине 19 в., когда в химическом анализе доминирующее положение занял «мокрый метод», т. е. анализ в растворах, главным образом водных, предметом А. х. стало изучение только таких реакций, которые дают аналитически ценный характерный продукт - нерастворимое или окрашенное соединение, возникающее в ходе быстрой реакции. В 1894 немецкий учёный В. Оствальд впервые изложил научные основы А. х. как теорию химического равновесия ионных реакций в водных растворах. Эта теория, дополненная результатами всего последующего развития ионной теории, стала основой А. х. Работами русских химиков М. А. Ильинского и Л. А. Чугаева (конец 19 в. - начало 20 в.) было положено начало применению органических реактивов, характеризующихся большой специфичностью и чувствительностью, в неорганическом анализе. Исследования показали, что для каждого неорганического иона характерна химическая реакция с органическим соединением, содержащим определённую функциональную группировку (т. н. функционально-аналитическую группу). Начиная с 20-х гг. 20 в. в химическом анализе стала возрастать роль инструментальных методов, снова возвращавших анализ к исследованию физических свойств анализируемых веществ, но не тех макроскопических свойств, которыми оперировал анализ в период до создания научной химии, а атомных и молекулярных свойств. Современная А. х. широко пользуется атомными и молекулярными спектрами излучения и поглощения (видимые, ультрафиолетовые, инфракрасные, рентгеновские, радиочастотные и гамма-спектры), радиоактивностью (естественная и искусственная), масс-спектрометрией изотопов, электрохимическими свойствами ионов и молекул, адсорбционными свойствами и др. (см. , , , , , , , , , ) .Применение методов анализа, основанных на этих свойствах, одинаково успешно в неорганическом и органическом анализе. Эти методы значительно углубляют возможности расшифровки состава и структуры химических соединений, качественного и количественного их определения; они позволяют доводить чувствительность определения до 10 -12- 10 -15% примеси, требуют малого количества анализируемого вещества, часто могут служить для т. н. неразрушающего контроля (т. е. не сопровождающегося разрушением пробы вещества), могут служить основой для автоматизации процессов производственного анализа. Вместе с тем широкое распространение этих инструментальных методов ставит новые задачи перед А. х. как наукой, требует обобщения методов анализа не только на основе теории химических реакций, но и на основе физической теории строения атомов и молекул. А. х., выполняющая важную роль в прогрессе химической науки, имеет также огромное значение в контроле промышленных процессов и в сельском хозяйстве. Развитие А. х. в СССР тесно связано с индустриализацией страны и последующим общим прогрессом. Во многих вузах организованы кафедры А. х., готовящие высококвалифицированных химиков-аналитиков. Советские учёные разрабатывают теоретические основы А. х. и новые методы для решения научных и практических задач. С возникновением таких отраслей, как атомная промышленность, электроника, производство полупроводников, редких металлов, космохимия, одновременно появилась необходимость разработки новых тонких и тончайших методов контроля чистоты материалов, где во многих случаях содержание примесей не должно превышать одного атома на 1-10 млн. атомов производимого продукта. Все эти проблемы успешно решаются советскими химиками-аналитиками. Совершенствуются также и старые методы химического контроля производства. Развитие А. х. как особой отрасли химии вызвало к жизни и издание специальных аналитических журналов во всех промышленно развитых странах мира. В СССР издаются 2 таких журнала - «Заводская лаборатория» (с 1932) и «Журнал аналитической химии» (с 1946). Имеются и специализированные международные журналы по отдельным разделам А. х., например журналы по хроматографии и по электроаналитической химии. Специалистов по А. х. готовят на специальных отделениях университетов, химико-технологических техникумов и профессионально -технических училищ. Лит.:Алексеев В. Н., Курс качественного химического полумнкроанализа, 4 изд., М. 1962: его же. Количественный анализ, 2 изд. , М., 1958; Ляликов Ю.С., Физико-химические методы анализа, 4 изд., М., 1964; Юйнг Г. Д. .Инструментальные методы химического анализа, пер. с англ., М., 1960; Лурье Ю. Ю., Справочник по аналитической химии, М., 1962. Ю. А. Клячко. Аналитические счета Аналити'ческие счета',см. . Аналитические формы Аналити'ческие фо'рмыв языке, сложные, описательные словосочетания, состоящие из вспомогательного и полнозначного слова и функционирующие в качестве грамматической формы последнего («буду читать» - А. ф. будущего времени глагола «читать», «самый красивый» - А. ф. превосходной степени прилагательного «красивый»; англ. I have seen, франц. J'ai vu, нем. Ich habe gesehen - «видел»). А. ф. имеют то же лексическое значение, что и входящее в них полнозначное слово, либо отличаясь от него дополнительным смысловым оттенком, либо выражая определённые отношения между ним и др. членами предложения. Вспомогательное слово А. ф. не должно присоединять дополнительное лексическое значение к полнозначному слову (словосочетание «начну читать» не принадлежит к А. ф. глагола «читать», поскольку слово «начну» вносит дополнительное значение начала действия). Вспомогательное слово является постоянной, а полнозначное - переменной частью А. ф., что обеспечивает продуктивность А. ф. А. ф. часто функционируют параллельно с ,образуя эквивалентные грамматические формы («красивее» и «более красивый» - соответственно, синтетические и А. ф. сравнительной степени прилагательного «красивый»). А. ф. слов находятся в регулярном соответствии с другими грамматическими формами этих слов и заполняют определённый пробел в структуре языка. Иногда к А. ф. относят словосочетания, выражающие грамматические формы (А. ф. падежа: англ. to the father, франц. au pйre - «отцу»). Лит.:Смирницкий А. И., Аналитические формы, «Вопросы языкознания», 1956, N° 2: Гухман М. М., Глагольные аналитические конструкции как особый тип сочетаний частичного или полного слова, в кн.: Вопросы грамматического строя, М., 1955: Аналитические конструкции в языках различных типов, М., 1965. Аналитические функции Аналити'ческие фу'нкции,функции, которые могут быть представлены .Исключительная важность класса А. ф. определяется следующим. Во-первых, этот класс достаточно широк; он охватывает большинство функций, встречающихся в основных вопросах математики и её приложений к естествознанию и технике. Аналитическими являются -многочлены, рациональные функции, показательная и логарифмическая, степенная, тригонометрические и обратные тригонометрические, гиперболические и им обратные, алгебраические функции, и -эллиптические, цилиндрические и др. Во-вторых, класс А. ф. замкнут относительно основных операций арифметики, алгебры и анализа; применение арифметических действий к функциям этого класса, решение алгебраических уравнений с аналитическими коэффициентами, дифференцирование и интегрирование А. ф. приводят снова к А. ф. Наконец, А. ф. обладают важным свойством единственности; каждая А. ф. образует одно «органически связанное целое», представляет собой «единую» функцию во всей своей естественной области существования. Это свойство, которое в 18 в. считалось неотделимым от самого понятия ,приобрело принципиальное значение после установления в 1-й половине 19 в. общей точки зрения на функцию как на произвольное соответствие. Теория А. ф. создана в 19 в., в первую очередь благодаря работам О. ,Б. и К. .Решающую роль в построении этой теории сыграл «выход в комплексную область» - переход от действительного переменного хк комплексному переменному z= х + iy,которое может меняться в произвольной области комплексной плоскости. Теория А. ф. возникла как теория функций комплексного переменного; в некотором смысле именно аналитические (а не произвольные комплексные функции двух действительных переменных хи y) естественно считать функциями комплексного переменного z.Теория А. ф. составляет основное содержание общей теории функций комплексного переменного. Поэтому часто под теорией функций комплексного переменного понимают именно теорию А. ф. Существуют различные подходы к понятию аналитичности. В основе одного из них, впервые развитого Коши и далеко продвинутого Риманом, лежит структурное свойство функции - существование производной по комплексному переменному, или комплексная дифференцируемость. Этот подход тесно связан с геометрическими соображениям и. Другой подход, систематически развивавшийся Вейерштрассом, основывается на возможности представления функций степенными рядами; он связан, тем самым, с аналитическим аппаратом, которым может быть изображена функция. Основной факт теории А. ф. заключается в тождественности соответствующих классов функций, рассматриваемых в произвольной области комплексной плоскости. Приведём точные определения. Всюду в дальнейшем через z обозначается комплексное число х + iy, где xи y- действительные числа. Геометрически число zизображается точкой плоскости с координатами хи y;евклидова плоскость, точки которой отождествляются с комплексными числами, называется комплексной плоскостью. Пусть D -область (открытое связное множество) в комплексной плоскости. Если каждой точке zобласти Dприведено в соответствие некоторое комплексное число w,то говорят, что в области Dопределена (однозначная) функция f комплексного переменного z,и пишут: w = f( z) , z( D.Функция w = f( z) = f( x+ iy) комплексного переменного z( Dможет рассматриваться как комплексная функция двух действительных переменных хи y,определённая в области D.Полагая w = u + iv,где uи v- действительные числа, замечают, что задание такой функции fэквивалентно заданию двух действительных функций j и y двух действительных переменных хи y,определённых в той же области: u =j( x, y) , v =y( x, y) ,( x, y)О D. Пусть z -фиксированная точка области D. Придадим zпроизвольное приращение D z= D x+ iD y(так, чтобы точка z+D zоставалась в пределах области D) и рассмотрим соответствующее приращение функции f: D f( z) = f( z +( z) - f( z) .Если разностное отношение D f( z)/D zимеет предел при Dz®0, т. е. существует комплексное число Атакое, что для любого e > 0 будет пD f( z)/D z- Aп < e как только пDzп < d (d = d(e) > 0), то функция fназывается моногенной в точке z,а число А -её производной в этой точке: А = f'( z) = df( z)/ dz.Функция, моногенная в каждой точке области D,называется моногенной в области D. Если функция f моногенна в точке zО D,то f и соответствующие функции j и y имеют в этой точке частные производные по хи y;при этом ¶ f/¶ x =¶y/¶x + i(¶y/¶x), ¶ f/¶y = ¶j/¶y + i(¶y/¶y) .Производную f’( z) можно выразить через частные производные fпо хи по у(достаточно вычислить предел отношения D f( z)/D zдвумя разными способами - при D z= Dx ® 0 и при D z= iD y® 0; приравнивая соответствующие выражения, получаем ¶ f/¶ x= (1/ i)¶ f/¶ yили, что то же самое, ¶ f/¶ x+ i(¶ f/¶ y) = 0. Переходя к функциям j и y, это равенство можно переписать так: ¶j/¶ x= ¶y/¶ y, ¶j/¶ y= - ¶y/¶ x. Если функция fмоногенна в области D,то последние соотношения справедливы в каждой точке области D;они называются уравнениями Коши - Римана. Следует отметить, что эти уравнения встречались уже в 18 в. в связи с изучением функций комплексного переменного в трудах и Л. . Моногенность функции
fэквивалентна её дифференцируемости в смысле комплексного анализа. При этом под дифференцируемостыо
fв точке
zО
Dпонимается возможность представления её приращения в виде D
f(
z) =
AD
z+ a(D
z)D
z, где a(Dz) ® 0 при D
z® 0; дифференциал
df(
z)
функции
fв точке
z,равный главной части
AD
zеё приращения D
f(
z), в этом случае пропорционален
dz =D
zи имеет вид
f’(
z)
dz.Полезно сравнить понятия дифференцируемости функции
f- в смысле действительного анализа и в смысле комплексного анализа. В первом случае дифференциал
dfимеет вид (¶
f/¶
x)
dx+ (¶
f/¶
y)
dy.Удобно переписать это выражение в комплексной форме. Для этого переходят от независимых переменных
x, ук переменным z
,
Отсюда уже нетрудно заключить, что дифференцируемость функции
fв смысле комплексного анализа имеет место в том и только том случае, когда она дифференцируема в смысле действительного анализа и справедливо равенство ¶f/¶
¶ f/¶ z= f’= df/ dz.
Равенство ¶f/¶
Интеграл от функции f =j + iy вдоль (ориентированной спрямляемой) кривой Г можно определить с помощью понятия криволинейного интеграла:
Центральное место в теории моногенных функций (теории Коши) занимает следующая итегральная теорема Коши: если функция моногенна в односвязной области D,то S Г f( z) dz= 0 для любой замкнутой кривой Г, лежащей в этой области. В произвольной области D то же утверждение справедливо для замкнутых кривых Г, которые непрерывной деформацией могут быть стянуты в точку (оставаясь в пределах области D) .Опираясь на интегральную теорему Коши, нетрудно доказать интегральную формулу Коши: если функция f моногенна в области Dи Г - простая замкнутая кривая, принадлежащая области Dвместе со своей внутренностью D Гто для любой точки zО D Г
(ориентация кривой Г предполагается положительной относительно области D Г) Пусть функция f моногенна в области D.Фиксируем произвольную точку z 0области Dи обозначим через g окружность с центром в точке z 0и радиусом r > 0, принадлежащую, вместе со всем кругом: К: Iz - z 0I < r, области D.Тогда
Представим ядро Коши 1/( t -z) для tОg и zО Kв виде суммы бесконечной геометрической прогрессии:
поэтому ряд сходится равномерно относительно tОg при любом фиксированном zО K,интегрируя этот ряд - после умножения на
-почленно, получают разложение функции fв степенной ряд
сходящийся в круге K: I z - z 0I < r. Уточним теперь понятие аналитичности. Пусть f- функция, определённая в области D;она называется аналитической (или голоморфной) в точке z 0области , если существует окрестность этой точки (круг с центром в z 0), в которой функция f представляется степенным рядом: f( z) = a 0+ a 1( z - z 0) + a 2( z- z 0) 2+. . . . + a n( z- z 0) n+ . . . Если это свойство имеет место в каждой точке z 0области D,то функция fназывается аналитической (голоморфной) в области D.
Выше было показано, что функция
f, моногенная в области
D,аналитична в этой области. В отдельной точке это утверждение неверно; например, функция
f(
z) = кzк
2= z
называется рядом Тейлора функции fв точке z 0. Тем самым, аналитичность функции fв области Dозначает, что в каждой точке области Dфункция fбесконечно дифференцируема и её ряд Тейлора сходится к ней в некоторой окрестности этой точки. Следовательно, понятия моногенности и аналитичности функции в области тождественны и каждое из следующих свойств функции fв области D -моногенность, дифференцируемость в смысле комплексного анализа, дифференцируемость в смысле действительного анализа вместе с выполнением уравнений Коши - Римана - может служить определением аналитичности fв этой области. Важнейшее свойство А. ф. выражается следующей теоремой единственности: две функции, аналитические в области Dи совпадающие на каком-либо множестве, имеющем предельную точку в D,совпадают и во всей области D(тождественны). В частности, аналитическая в области функция, отличная от тождественного нуля, может иметь в области лишь изолированные нули. Если Е -произвольное множество (в комплексной плоскости и, в частности, на действительной прямой), то функция f (z), zО E,называется аналитической на множестве E,если каждая точка этого множества имеет окрестность, на пересечении которой с множеством Ефункция f представляется сходящимся степенным рядом; это означает в действительности, что fаналитична на некотором открытом множестве, содержащем Е(точнее, существует открытое множество, содержащее Е,и аналитическая на нём функция, fсовпадающая с fна множестве E) .Для открытых множеств понятие аналитичности совпадает с понятием дифференцируемости по множеству (моногенности). Однако в общем случае это не так; в частности, на действительной прямой существуют функции, не только имеющие производную, но и бесконечно дифференцируемые в каждой точке, которые не являются аналитическими ни в одной точке этой прямой. Например,
С другой стороны, для справедливости теоремы единственности А. ф. существенно свойство связности множества E.Поэтому А. ф. рассматриваются обычно вобластях, т.е. на открытых и связных множествах. Важную роль в изучении А. ф. играют точки, в которых нарушается свойство аналитичности - т. н. А. ф. Рассмотрим здесь изолированные особые точки (однозначных) А. ф. Пусть f- А. ф. в области вида 0 < | z- z 0| < r; в этой области fразлагается в ряд Лорана:
содержащий, вообще говоря, не только положительные, но и отрицательные степени z - z 0.Если в этом разложении члены с отрицательными степенями отсутствуют ( a n= 0 для n = -1, -2,...), то z 0называется правильной точкой f. В правильной точке существует и конечен
полагая f( z 0) = a 0 ,получают функцию, аналитическую во всём круге пz - z 0п < r . Если ряд Лорана функции fсодержит лишь конечное число членов с отрицательными степенями z- z 0 :
то точка z 0называется полюсом функции f(порядка m); полюс z 0характеризуется тем, что
В случае, если ряд Лорана содержит бесконечное число отрицательных степеней z - z 0, то z 0называется существенно особой точкой; в таких точках не существует ни конечного, ни бесконечного предела функции f. Если z 0- изолированная особая точка функции f, то коэффициент a -1в её разложении в ряд Лорана называется функции fв точке z 0. Функции, представимые в виде отношения двух функций, аналитических в области D,называется мероморфными в области D.Мероморфная в области функция аналитична в этой области за исключением, быть может, конечного или счётного множества полюсов; в полюсах значения мероморфной функции считаются равными бесконечности. Если допустить такие значения, то мероморфные в области Dфункции могут быть определены как функции, которые в окрестности каждой точки z 0области Dпредставимы рядом по степеням z - z 0,содержащим конечное (зависящее от z 0) число членов с отрицательными степенями z - z 0. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47 |
|||||||
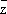 ,которые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями: z =
х+
iy,
,которые формально можно считать новыми независимыми переменными, связанными со старыми соотношениями: z =
х+
iy,
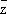 = x - iy(становясь на эту точку зрения, функцию
fиногда записывают в виде
f(z,
= x - iy(становясь на эту точку зрения, функцию
fиногда записывают в виде
f(z,
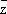 )
.Выражая
dxи
dyчерез
dzи
d
)
.Выражая
dxи
dyчерез
dzи
d
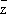 по обычным правилам вычисления дифференциалов, получают
df =(¶
f/¶
z)
dz+ (¶
f/¶
по обычным правилам вычисления дифференциалов, получают
df =(¶
f/¶
z)
dz+ (¶
f/¶
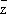 )
d
)
d
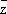 ,где ¶f/¶z
=(
1/
2) (¶f/¶x - i¶f/¶y) и ¶f/¶
,где ¶f/¶z
=(
1/
2) (¶f/¶x - i¶f/¶y) и ¶f/¶
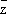 = (
1/
2) (¶f/¶x + i¶f/¶y) (формальные) производные функции
fпо
zи
= (
1/
2) (¶f/¶x + i¶f/¶y) (формальные) производные функции
fпо
zи
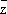 соответственно.
соответственно.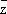 = 0
,являющееся краткой формой записи уравнений Коши - Римана; при этом
= 0
,являющееся краткой формой записи уравнений Коши - Римана; при этом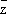 = 0 показывает, что дифференцируемыми в смысле комплексного анализа являются те и только те функции f, которые, рассматриваемые формально как функции независимых переменных
zи
= 0 показывает, что дифференцируемыми в смысле комплексного анализа являются те и только те функции f, которые, рассматриваемые формально как функции независимых переменных
zи
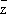 «зависят только от z», являются «функциями комплексного переменного z».
«зависят только от z», являются «функциями комплексного переменного z».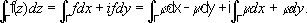
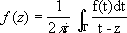
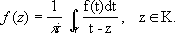
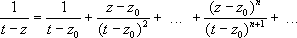
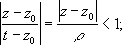
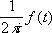
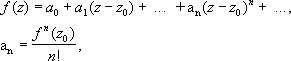
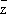 моногенна в точке
z
0= 0, но нигде не аналитична. С другой стороны, функция
f, аналитическая в точке
z
0области
D,моногенна в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема) по комплексному переменному
z; коэффициенты ряда могут быть выражены через производные функции
fв точке
z
0по формулам:
a
n=
f
(n)(
z
0)/
n!
.Степенной ряд, записанный в форме
моногенна в точке
z
0= 0, но нигде не аналитична. С другой стороны, функция
f, аналитическая в точке
z
0области
D,моногенна в этой точке. Более того, сумма сходящегося степенного ряда имеет производные всех порядков (бесконечно дифференцируема) по комплексному переменному
z; коэффициенты ряда могут быть выражены через производные функции
fв точке
z
0по формулам:
a
n=
f
(n)(
z
0)/
n!
.Степенной ряд, записанный в форме