 |
|
Популярные авторы:: БСЭ :: Говард Роберт Ирвин :: Лесков Николай Семёнович :: Картленд Барбара :: Чехов Антон Павлович :: Раззаков Федор :: Нортон Андрэ :: Лондон Джек :: Толстой Лев Николаевич :: Эллисон Харлан Популярные книги:: Справочник по реестру Windows XP :: Черные очки :: Бурый волк :: На тебе греха не будет... :: Воздушный шарик – Шарик-миротворец :: Амок :: Партия в триктрак :: Разведение cобак :: Герцог Сорвиголова :: Случай богородицы |
Большая Советская Энциклопедия (ОП)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ОП) - Чтение (стр. 4)
Результат последовательного применения
праз одного и того же оператора
Аесть
n-
ястепень
A
nэтого оператора. Например,
n-я степень оператора дифференцирования есть оператор
n-kpaтного дифференцирования D
n
[
f (t)]=
f
(n)(t).Произведение l
Аоператора
Ана число l определяется формулой
(l А)( х) =l А( х). Оператор Е, переводящий всякий элемент хв самого себя, называется единичным. Нулевым называется оператор О, переводящий каждый элемент в нуль. Очевидно, что при любом Асправедливы равенства: AE = EA = Аи А+О =О + А = А, далее, если, А –1существует, то А –1 А= AA –1 = Е(следует заметить, что для двух произвольных операторов Аи Впроизведения ABи BA, вообще говоря, не равны между собой). С помощью операций сложения, умножения операторов и умножения операторов на числа можно определить многочлены от линейного оператора, а путём предельного перехода, понимаемого соответствующим образом, - и более сложные функции от оператора. Например, если D- оператор дифференцирования, то e Dозначает оператор, определяемый формулой
имеющий смысл для тех f( t), для которых ряд справа сходится. Для аналитических функций сумма этого ряда равна f( t+ 1), т. е. e D- оператор сдвига, переводящий f( t) в f( t +1). Линейные операторы в гильбертовом пространстве. Наиболее полно О. т. разработана для случая линейных операторов в гильбертовом пространстве . Пусть А- ограниченный линейный оператор в гильбертовом пространстве H. Комплексное число l называется собственным значением оператора А, если существует такой элемент х¹ 0 из H, что А( х) =l х; при этом хназывается собственным вектором оператора А, отвечающим данному собственному значению. Число l называется регулярной точкой оператора А, если оператор ( А +l Е) –1существует, определён на всём Ни ограничен; остальные значения l называется точками спектра оператора А. Каждое собственное значение принадлежит спектру, их совокупность образует точечный спектр, остальную часть спектра называется непрерывным спектром. Тот факт, что спектр линейного оператора, вообще говоря, не исчерпывается его собственными значениями, представляет собой характерную черту линейных операторов в бесконечномерном пространстве, отличающую их от линейных преобразований конечномерного евклидова пространства. Оператор А* называется сопряжённым к А, если скалярное произведение ( Ax, у) =( х, А* у) для всех хи уиз Н. Оператор Аназывается самосопряжённым, если А= А*, и унитарным, если А*= А –1. Самосопряжённые и унитарные операторы представляют собой важнейшие и наиболее полно изученные классы линейных операторов в гильбертовом пространстве. Их теория является обобщением теории самосопряжённых и унитарных линейных преобразований n-мерного евклидова пространства. См. также Спектральный анализ (математический). Одним из простейших классов ограниченных линейных операторов в гильбертовом пространстве являются вполне непрерывные операторы. Оператор Аназывается вполне непрерывным, если он переводит всякое ограниченное множество из Нв компактное (см. Компактность ). Спектр вполне непрерывного оператора состоит из конечного или бесконечного счётного числа собственных значений и не имеет отличных от нуля предельных точек. Каждому l ¹ 0 отвечает лишь конечное число линейно независимых собственных функций. Непрерывный спектр отсутствует. Самосопряжённый вполне непрерывный оператор Аимеет хотя бы одно собственное значение, причём в Нможно выбрать полную ортогональную систему элементов, состоящую из собственных функций оператора А. Неограниченные операторы. Понятие ограниченного линейного оператора оказывается во многих случаях слишком узким. Поэтому возникла необходимость рассматривать т. н. неограниченные операторы. Соответствующее, более общее, определение гласит: оператор Аназывается линейным неограниченным оператором в гильбертовом пространстве Н, если: 1) соответствие у = А( х) определено для всех х, принадлежащих некоторому линейному многообразию W, называемому областью определения оператора A; 2) А(a х+ b y) = a А( х) +b A( y). Важнейшим классом неограниченных линейных операторов в гильбертовом пространстве являются дифференциальные операторы. Многие задачи математической физики, в частности теории колебаний, приводят к задаче о разыскании собственных функций и собственных значений различных дифференциальных операторов. Например, цилиндрические функции , Лежандра многочлены и т.д. представляют собой не что иное, как собственные функции определённых дифференциальных операторов. Нелинейные операторы. При изучении операторов предположение об их линейности играет весьма существенную роль. Однако в ряде случаев приходится рассматривать и нелинейные операторы. В частности, важное значение в механике и физике имеют нелинейные интегральные уравнения. Лит.:Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972; Данфорд Н., Шварц Дж. Т., Линейные операторы. Общая теория, пер. с англ., М., 1962. Операторский транспорт Опера'торский тра'нспортв кинематографии и телевидении, предназначен для перемещения оператора и съёмочной аппаратуры в процессе киносъёмок либо телевизионных передач. О. т. применяется при съёмках в движении и для облегчения переходов от одной точки съёмки к другой. К средствам О. т. относятся операторские тележки ( рис. 1 ), краны ( рис. 2, 3), в отдельных случаях - специально оборудованные автомобили, вертолёты, лодки, сани, плоты и др. Операторские тележки используются для перемещения точки съёмки по горизонтали с незначительным изменением (в пределах 1,5 м) высоты установки киносъёмочного аппарата или телевизионной передающей камеры . Операторские краны применяются в тех случаях, когда необходимы значит. изменения положения точки съёмки в пространстве. В зависимости от высоты подъёма стрелы различают малые (до 2 мотносительно уровня земли), средние (от 2 до 4 м) и большие (свыше 4 м) краны. Операторские краны изготавливают с электроприводом всех движений стрелы. Большие операторские автомобили обычно оборудуются на базе либо легковых автомобилей высшего класса, имеющих наиболее спокойный ход, либо легковых вездеходов, позволяющих вести съёмку при движении по плохим дорогам. Лит.:Головня Е. В., Киносъемки с движения, М., 1940; Григорьев В. И. Специальные приспособления и устройства для съемки динамических панорам, «Техника кино и телевидения», 1970, № 6. В. Б. Толмачев. 
Рис. 3. Средний операторский кран, установленный на грузовом автомобиле. 
Рис. 1. Операторская тележка с механизированным гидравлическим подъёмом штатива, на котором утановлен киносъёмочный аппарат. 
Рис. 2. Малый операторский кран типа 2МКТ с пневмагидравлическим приводом. Операторское искусство Опера'торское иску'сство, кинематографический вид творчества; создание совместно с режиссёром и художником методами киносъёмки художественно-изобразительной формы кинофильма и телевизионного фильма. В зрительных образах раскрываются содержание и идея произведения, замысел кинодраматурга и режиссёра. В кадре - необычайно пластичной изобразительной форме - могут быть изображены предмет и его детали, явление и его отдельные элементы, переданы выразительность мимики и жеста, различные виды движения, его темп и скорость, выполнены оптические «укрупнения» и др. Сцены и эпизоды фильма представляют собой изобразительно-монтажную композицию, как бы «вертикальную картину», развёртывающуюся на экране, время показа каждого монтажного кадра ограничено, поэтому важно оптически организовать и направить внимание зрителя, создать «эффект присутствия». Для решения этой задачи применяются съёмки движущимся киносъёмочным аппаратом, особые ракурсы, эффекты освещения и киноперспективы, вариооптика (трансфокаторы). В зависимости от специфики отдельных сцен и эпизодов в О. и. используются принципы других изобразительных искусств и художественных жанров - живописи, графики, пейзажа, портрета, батального, бытового и исторического жанров. О. и. во многом определяет выразительность экранных образов. Основой операторского мастерства является художественное освещение объектов киносъёмки - актёрских мизансцен, архитектурных форм, декораций, интерьера. Обрисовывая светотенью пластические формы фигур, жест и мимику актёра, обозначая освещением место и время действия, оператор решает светотональную и цветовую композиции каждой сцены, «настроение» эпизода. Кинокамера воссоздаёт на экране цвет и фактуру материалов, объёмно-пластическую форму фигур в движении, поэтому применяются различные степени яркости освещения как в черно-белом, так и в цветном киноизображении с целью выявления объёмности предметов, создания иллюзии глубины пространства и др. Важная роль в О. и. принадлежит композиции кадра - одному из методов организации киноматериала, дающему возможность наиболее полно воплотить идеи и образы фильма; раздельно поставленные и снятые монтажные кадры координируются по развитию действия и по изобразительной форме: по движению объектов съёмки и киносъёмочного аппарата, по ракурсам, цвету, освещению, колориту и др. Возникновение и развитие О. и. тесно связаны со становлением киноискусства . Самые ранние фильмы представляли собой «живые фотографии». Постепенно в разнообразных по жанрам кинолентах выявилось богатство возможностей и значение О. и. В выдающихся советских фильмах, снятых в 20-е гг., - «Броненосец “Потемкин”» (оператор Э. К. Тиссэ), «Мать» (оператор А. Д. Головня) и др., крупные планы, ракурсные съёмки, новаторские приёмы освещения были использованы для воспроизведения динамики революционные действия, создания образов людей революции. В стремлении к овладению новыми средствами выразительности для воплощения событий революционной истории и современности формировалась советская школа О. и. В 30-е гг. в кинокартинах «Земля» (оператор Д. П. Демуцкий), «Чапаев» (оператор А. И. Сигаев), трилогии о Максиме (оператор А. Н. Москвин), «Ленин в Октябре» и «Ленин в 1918 году» (оператор Б. И. Волчек) и др. О. и. достигло высокого художественного уровня в батальных сценах, живописного мастерства в кинопортрете и жанровых эпизодах. С середины 50-х гг. одновременно с внедрением новых систем кинематографа, в том числе широкоэкранного и широкоформатного, совершенствуются и изобразит. возможности О. и. Создаются художественно-значительные по операторскому решению и мастерству фильмы: «Отелло» (оператор Е. Н. Андриканис), «Летят журавли» (оператор С. П. Урусевский), «Иваново детство» (оператор В. И. Юсов), «Дневные звёзды» и «Чайковский» (оператор М. М. Пилихина), «Война и мир» (оператор А. А. Петрицкий), «У озера» (оператор В. А. Рапопорт), «Белая птица с чёрной отметиной» (оператор Ю. Г. Ильенко), «Освобождение» (оператор И. М. Слабневич), «Невестка» (оператор Х. К. Нарлиев), «Укрощение огня» (оператор С. А. Вронский) и многие др. Интенсивное развитие системы выразительных средств характерно и для телефильмов, в которых основное внимание сосредоточивается на возможности максимально глубоко и убедительно раскрыть внутренний мир человека; особенно показательны телефильмы «Адъютант его превосходительства» (оператор П. Н. Терпсихоров) и «Семнадцать мгновений весны» (оператор П. В. Катаев). Массовый характер, стремительный рост кинематографии и телевидения, расширение тематики и жанров фильмов определяют и рост требований к художественно-изобразительной культуре, её органическому подчинению идейной направленности произведения; большое значение приобретают все компоненты О. и. - портретные характеристики персонажей, светотональное и колористическое решение, фотографическое и техническое качество изображения и др. Метод социалистического реализма предоставляет деятелям советской школы О. и. возможности полного раскрытия творческой индивидуальности, применения новаторских приёмов киновыразительности как необходимого условия воссоздания действительности в ярких и убедительных художественных образах. Развитию О. и. в капиталистических странах большой ущерб наносили ремесленничество, стандартизация изобразительной формы, насаждавшиеся кинопредпринимателями, влияние антиреалистических тенденций, голливудских эстетических норм в выборе планов, композиций мизансцен, схем освещения. Однако лучшие представители О. и. стремились обогащать и совершенствовать своё мастерство, правдиво отражать жизнь, развивать прогрессивные традиции национального изобразительного искусства. Большой вклад в О. и. разных периодов развития кинематографа внесли операторы Германии, Франции, США, Италии, Мексики, Японии. Значительных успехов достигли мастера О. и. Польши и др. зарубежных социалистических стран. Лит.:Головня А., Свет в искусстве оператора, М., 1945; его же, Мастерство кинооператора, М., 1965; Косматов Л., Операторское мастерство, М., 1962; его же, Свет в интерьере, М., 1973; Ильин Р. Н., Изобразительные ресурсы экрана, М., 1973. А. Д. Головня. Операторы
Опера'торыв квантовой теории, математическое понятие, широко используемое в математическом аппарате
квантовой механики
и
квантовой теории поля
и служащее для сопоставления определённому вектору состояния (или волновой функции) y др. определённых векторов (функций) y'. Соотношение между y и y' записывается в виде y
'=
Простейшие виды О., действующих на волновую функцию y(
х) (где
х- координата частицы), - О. умножения (например, О. координаты
В квантовой механике в основном используются
линейные операторы
. Это означает, что они обладают следующим свойством: если
Существенные свойства О.
Собственные функции и собственные значения О. физических величин должны удовлетворять определённым требованиям. Т. к. непосредственно измеряемые физич. величины всегда принимают веществ. значения, то соответствующие квантовомеханич. О. должны иметь веществ. собств. значения. Далее, поскольку в результате измерения физич. величины в любом состоянии y должно получаться одно из возможных собств. значений этой величины, необходимо, чтобы произвольная волновая функция (вектор состояния) могла быть представлена в виде линейной комбинации собств. функций (векторов) y n О. этой физич. величины; др. словами, совокупность собств. функций (векторов) должна представлять полную систему. Этими свойствами обладают собств. функции и собств. значения т.н. самосопряжённых О., или эрмитовых операторов .
С О. можно производить алгебраич. действия. В частности, под произведением О.
Уравнения квантовой механики могут быть формально записаны точно в том же виде, что и уравнения классической механики (гейзенберговское представление в квантовой механике), если заменить физические величины, входящие в уравнения классической механики, соответствующими им О. Всё различие между квантовой и классической механикой сведется тогда к различию алгебр. Поэтому О. в квантовой механике иногда называют q-числами, в отличие от с-чисел, т. е. обыкновенных чисел, с которыми имеет дело классическая механика. О. можно не только умножать, но и возводить в степень, образовывать из них ряды и рассматривать функции от О. Произведение эрмитовых О. в общем случае не является эрмитовым. В квантовой механике используются и неэрмитовы О., важным классом которых являются унитарные операторы . Унитарные О. не меняют норм («длин») векторов и «углов» между ними. Неизменность нормы вектора состояния даёт возможность интерпретации его компонент как амплитуд вероятности равным образом в исходной и преобразованной функции. Поэтому действием унитарного О. описывается развитие квантовомеханической системы во времени, а также её смещение как целого в пространстве, поворот, зеркальное отражение и др. Выполняемые унитарными О. преобразования (унитарные преобразования) играют в квантовой механике такую же роль, какую в классической механике играют канонические преобразования (см. Механики уравнения канонические ). В квантовой механике применяется также О. комплексного сопряжения, не являющийся линейным. Произведение такого О. на унитарный О. называются антиунитарным О. Антиунитарные О. описывают преобразование обращения времени и некоторые др. В теории квантовых систем, состоящих из тождественных частиц, широко применяется метод
квантования вторичного
, в котором рассматриваются состояния с неопределённым или переменным числом частиц и вводятся О., действие которых на вектор состояния с данным числом частиц приводит к вектору состояния с измененным на единицу числом частиц (О. рождения и поглощения частиц). О. рождения или поглощения частицы в данной точке
х,
Лит. см. при статьях Квантовая механика , Квантовая теория поля . В. Б. Берестецкий. Операций исследование Опера'ций иссле'дование, научный метод выработки количественно обоснованных рекомендаций по принятию решений. Важность количественного фактора в О. и. и целенаправленность вырабатываемых рекомендаций позволяют определить О. и. как теорию принятия оптимальных решений. О. и. способствует превращению искусства принятия решений в научную и притом математическую дисциплину. Термин «О. и.» возник в результате буквального перевода американского выражения operations research, являющегося модификацией английского operational research, введённого в конце 30-х гг. 20 в. как условное наименование одного из подразделений британских ВВС, занимавшегося вопросами использования радиолокационных установок в общей системе обороны. Описание всякой задачи О. и. включает задание компонент (факторов) решения (которые можно понимать как его непосредственные последствия; обычно, хотя и необязательно, компоненты решения являются численными переменными), налагаемых на них ограничений (отражающих ограниченность ресурсов) и системы целей. Всякая система компонент решения, удовлетворяющих всем ограничениям, называется допустимым решением. Каждой из целей соответствует целевая функция, заданная на множестве допустимых решений, значения которой выражают меру осуществления цели. Сущность задачи О. и. состоит в нахождении наиболее целесообразных, оптимальных решений. Поэтому задачи О. и. обычно называются оптимизационными. Некоторые наиболее важные и разработанные задачи О. и. получили название моделей О. и. Они обычно выделяются содержательной терминологией и имеют специфические методы решения. К их числу относятся транспортная задача , задача размещения, теория надёжности , близкая к ней теория замены оборудования, теория расписаний (называется также теорией календарного планирования), теория управления запасами и теория сетевого планирования . Одной из моделей О. и. считается массового обслуживания теория , хотя ещё не все её задачи приобрели оптимизационный характер. Среди задач О. и. выделяются те, в которых имеется одна целевая функция, принимающая численные значения. Теория таких задач называется математическим программированием (или оптимальным программированием). Им противостоят задачи с несколькими целевыми функциями или с одной целевой функцией, но принимающей векторные значения или значения ещё более сложной природы. Эти задачи называются многокритериальными. Они решаются путём сведения (часто условного) к задачам с единственной целевой функцией либо на основе использования игр теории . Принятие решений происходит на основе информации, поступающей к принимающему решение субъекту. Поэтому задачи О. и. естественно классифицировать по их теоретико-информационным свойствам. Если субъект в ходе принятия решения сохраняет своё информационное состояние, т. е. никакой информации не приобретает и не утрачивает, то принятие решения можно рассматривать как мгновенный акт. Соответствующие задачи О. и. называется статическими. Напротив, если субъект в ходе принятия решения изменяет своё информационное состояние, получая или теряя информацию, то в такой динамической задаче обычно целесообразно принимать решение поэтапно («многошаговые решения») или даже развёртывать принятие решения в непрерывный во времени процесс. Значительная часть теории динамических задач О. и входит в динамическое программирование . Соотношение между информационным состоянием субъекта и его истинным («физическим») состоянием может быть различным. Если информационное состояние охватывает целое множество истинных состояний (субъект знает, что он находится в одном из состояний этого множества, но более точно определить своё истинное состояние не может), то задача принятия решения называется неопределённой и решается методами теории игр. Если информационное состояние состоит из нескольких истинных состояний, но субъект, кроме того, знает («априорные») вероятности каждого из истинных состояний, то задача называется стохастической (вероятностной) и решается методами стохастического программирования. Наконец, если информационное состояние совпадает с истинным, то задача называется детерминированной. При решении детерминированных задач важную роль играет аналитический вид ограничений и целевой функции. Так, если целевая функция есть линейная форма компонент решения, а ограничения описываются линейными неравенствами, то задача относится к линейному программированию . Остальные детерминированные задачи рассматриваются в нелинейном программировании, в котором естественно выделяются выпуклое программирование и квадратичное программирование. Если по условиям задачи компоненты решения могут принимать лишь целые значения, то задачу относят к целочисленному (дискретному) программированию. Семейство задач, зависящих от параметра, иногда объединяют в одну задачу параметрического программирования. Особым частным случаем детерминированных задач является нахождение минимакса (и максимина). Первоначально О. и. было связано с решением задач военного содержания, но уже с конца 40-х гг. сфера его приложений стала охватывать разнообразные стороны человеческой деятельности. О. и. используется для решения как чисто технических (особенно технологических), так и технико-экономических задач, а также задач управления на различных уровнях. Применение О. и. в практических оптимизационных задачах даёт значительный экономический эффект: по сравнению с традиционными «интуитивными» методами принятия решений увеличение выигрыша от использования оптимальных решений при одинаковых затратах около 10%. Лишь отдельные задачи О. и. поддаются аналитическому решению и сравнительно немногие - численному решению вручную. Поэтому рост возможностей О. и. тесно связан с прогрессом электронной вычислительной техники. В свою очередь потребности в решении задач О. и. влияют на рост и состав парка вычислительных машин. Т. к. для задач О. и. характерно большое количество числовых данных, составляющих их условия, для решения этих задач особенно приспособлены вычислительные машины, обладающие большой памятью. Практическое применение О. и. встречает ряд трудностей, возникающих уже при составлении задачи О. и. как модели и особенно при указании целевой функции. Серьёзными могут оказаться математические, в частности вычислительные, затруднения при нахождении оптимального решения задачи. В СССР и др. странах во многих университетах, высших технических учебных заведениях и институтах повышения квалификации читаются курсы по О. и. Издаются специальные журналы: «Operational Research Quarterly» (L., с 1950), «Operations Research» (Balt., с 1952), «Naval Research Logistics Quarterly» (Wash., с 1954), «Revue franзaise de recherche opйrationnelle» (P., с 1956). Международная федерация обществ О. и. (International Federation of Operational Research Societies - IFORS) каждые три года созывает международные конгрессы (первый был проведён в 1957 в Лондоне). 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 |
|||||||
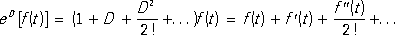 ,
,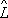 y, где
y, где
 - оператор. В квантовой механике физическим величинам (координате, импульсу, моменту количества движения, энергии и т.д.) ставятся в соответствие О.
- оператор. В квантовой механике физическим величинам (координате, импульсу, моменту количества движения, энергии и т.д.) ставятся в соответствие О.
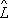 (О. координаты, О. импульса и т.д.), действующие на вектор состояния (или волновую функцию) y, т. е. на величину, описывающую состояние физической системы.
(О. координаты, О. импульса и т.д.), действующие на вектор состояния (или волновую функцию) y, т. е. на величину, описывающую состояние физической системы. ,
,
 y =
хy) и о. дифференцирования (например, О. импульса
y =
хy) и о. дифференцирования (например, О. импульса
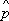 ,
,
 y
=
y
=
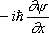 , где
i- мнимая единица,
, где
i- мнимая единица,
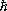 - постоянная Планка). Если y - вектор, компоненты которого можно представить в виде столбца чисел, то О. представляет собой квадратную таблицу -
матрицу
.
- постоянная Планка). Если y - вектор, компоненты которого можно представить в виде столбца чисел, то О. представляет собой квадратную таблицу -
матрицу
.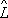 y
1
=y'
1и
y
1
=y'
1и
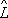 y
2
=
y'
2, то
y
2
=
y'
2, то
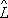 (
c
1y
1+
c
2y
2) =
c
1y'
1+
c
2y'
2, где
c
1и
с
2
- комплексные числа. Это свойство отражает
суперпозиции принцип
-
один из основных принципов квантовой механики.
(
c
1y
1+
c
2y
2) =
c
1y'
1+
c
2y'
2, где
c
1и
с
2
- комплексные числа. Это свойство отражает
суперпозиции принцип
-
один из основных принципов квантовой механики.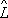 определяются уравнением
определяются уравнением
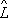 y
n
= l
n
y
n
, где l
n
- число. Решения этого уравнения y
n
называется собственными функциями (собственными векторами) оператора
y
n
= l
n
y
n
, где l
n
- число. Решения этого уравнения y
n
называется собственными функциями (собственными векторами) оператора
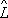 . Собственные волновые функции (собственные векторы состояния) описывают в квантовой механике такие состояния, в которых данная физическая величина
Lимеет определённое значение l
n
. Числа l
n
называется собственными значениями О.
. Собственные волновые функции (собственные векторы состояния) описывают в квантовой механике такие состояния, в которых данная физическая величина
Lимеет определённое значение l
n
. Числа l
n
называется собственными значениями О.
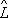 , а их совокупность - спектром О. Спектр может быть непрерывным или дискретным; в первом случае уравнение, определяющее y
n
, имеет решение при любом значении l
n
(в определённой области), во втором - решения существуют только при определённых дискретных значениях l
n
. Спектр О. может быть и смешанным: частично непрерывным, частично дискретным. Например, О. координаты и импульса имеют непрерывный спектр, а О. энергии в зависимости от характера действующих в системе сил - непрерывный, дискретный или смешанный спектр. Дискретные собственные значения О. энергии называются энергетическими уровнями.
, а их совокупность - спектром О. Спектр может быть непрерывным или дискретным; в первом случае уравнение, определяющее y
n
, имеет решение при любом значении l
n
(в определённой области), во втором - решения существуют только при определённых дискретных значениях l
n
. Спектр О. может быть и смешанным: частично непрерывным, частично дискретным. Например, О. координаты и импульса имеют непрерывный спектр, а О. энергии в зависимости от характера действующих в системе сил - непрерывный, дискретный или смешанный спектр. Дискретные собственные значения О. энергии называются энергетическими уровнями.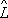 1и
1и
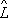 2понимается такой О.
2понимается такой О.
 =
=
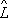 1
1
 2, действие которого на вектор (функцию) y даёт
2, действие которого на вектор (функцию) y даёт
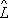 y = y’’, если
y = y’’, если
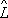 2y = y’ и
2y = y’ и
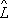 1y’
= y’’.
Произведение О. в общем случае зависит от порядка сомножителей, т.
е.
1y’
= y’’.
Произведение О. в общем случае зависит от порядка сомножителей, т.
е.
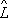 1
1
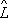 2
¹
2
¹
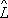 2
2
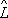 1. Этим алгебра О. отличается от обычной алгебры чисел. Возможность перестановки порядка сомножителей в произведении двух О. тесно связана с возможностью одновременного измерения физических величин, которым отвечают эти О. Необходимым и достаточным условием одновременной измеримости физических величин является равенство
1. Этим алгебра О. отличается от обычной алгебры чисел. Возможность перестановки порядка сомножителей в произведении двух О. тесно связана с возможностью одновременного измерения физических величин, которым отвечают эти О. Необходимым и достаточным условием одновременной измеримости физических величин является равенство
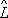 1
1
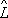 2
=
2
=
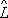 2
2
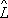 1(см.
Перестановочные соотношения
).
1(см.
Перестановочные соотношения
).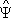 (
х) формально подобен волновой функции y(
х), как
q-и
с-числа, отвечающие одной и той же физической величине соответственно в квантовой и классической механике. Такие О. образуют квантованные поля, играющие фундаментальную роль в релятивистских квантовых теориях (квантовой электродинамике, теории элементарных частиц; см.
Квантовая теория поля
).
(
х) формально подобен волновой функции y(
х), как
q-и
с-числа, отвечающие одной и той же физической величине соответственно в квантовой и классической механике. Такие О. образуют квантованные поля, играющие фундаментальную роль в релятивистских квантовых теориях (квантовой электродинамике, теории элементарных частиц; см.
Квантовая теория поля
).