Большая Советская Энциклопедия (УР)
ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (УР) - Чтение
(стр. 1)
|
Автор:
|
БСЭ |
|
Жанр:
|
Энциклопедии |
|
-
Читать книгу полностью
(382 Кб)
- Скачать в формате fb2
(3,00 Мб)
- Скачать в формате doc
(162 Кб)
- Скачать в формате txt
(150 Кб)
- Скачать в формате html
(3,00 Мб)
- Страницы:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
|
|
Большая Советская Энциклопедия (УР)
Ур
Ур(шумер. Урим), древний город-государство на месте современного городища Тель-Мукайяр, в 20
кмк Ю.-З. от г. Насирия в Ираке. Первое поселение на месте У. возникло в конце 5-го тыс. до н. э., когда здесь была распространена расписная керамика типа
.В 4-м тыс., в период Урука, произошло становление У. как города. В 25 в. до н. э., в период 1 династии Ура (правители Месанспада, Аанепада и др.), представлял собой сильное государство. В течение 24–22 вв. (с небольшими перерывами) был подчинён соседним городам-государствам
,
,
,затем царству
,кутиям. Около 21 в. стал столицей «царства Шумера и Аккада» (III династия Ура). При царе Ур-Намму (21 в.) были созданы, возможно, самые древние в Двуречье писаные законы. Для этого периода истории У. характерно наличие больших царских хозяйств с фактически рабовладельческой эксплуатацией подневольных работников. Создавались идеологические основы деспотической царской власти (единая система пантеона, учение о вечности «царственности» и т.д.). Четыре следующих царя III династии Ура (Шульги, Амар-Суэн, Шу-Суэн, Ибби-Суэн) были обожествлены при жизни. Государство III династии Ура пало около 2000 до н. э. в ходе войны с аморитами и Эламом. У. оставался важным торгово-ремесленным центром, находясь под властью вавилонского (с 18 по 6 вв.) и ахеменидского (с 6 в.) царств. К концу 4 в. до н. э. У. пришёл в упадок. У. раскапывался англ. учёными Д. Тейлором в 1854, Р. Кэмпбелл-Томпсоном в 1918, Г. Р. Холлом в 1919–22 и особенно широко – англо-амер. экспедицией под руководством Ч. Л.
в 1922–34. Наиболее многочисленные и интересные памятники, вскрытые раскопками, датируются временем правления в У. I и III династий. Ко времени правления 1 династии (25 в. до н. э.) относятся 16 царских (?) гробниц, в которых были найдены многочисленные образцы роскошной утвари (из золота, серебра, алебастра, ляпис-лазури, обсидиана и др. материалов, иногда – с применением мозаичной техники). У. времени III династии (21 в. до н. э.) представлял собой в плане неправильный овал, окруженный кирпичной стеной. Среди сохранившихся фрагментарно кирпичных зданий этого времени – остатки дворца, храмового комплекса, в центре которого находился четырёхъярусный зиккурат, и др. сооружений. О художественной культуре У. см. также в ст.
.
Лит.:Тюменев А. И., Государственное хозяйство древнего Шумера, М. – Л., 1956; Вулли Л., Ур халдеев, пер. с англ., М., 1961; Gadd C. J., The history and monuments of Ur, L., 1929; Ur excavations, v. 1–5, 8–10, Oxf. – L., 1927–62; Ur excavations texts, fv. 1–6, L., 1928–63.
И. М. Дьяконов.
Ур. Голова быка с арфы из «царской гробницы». Золото, лазурит. 25 в. до н. э. Университет. Филадельфия.
Ураба
Ураба'(Uraba), залив Карибского моря, у берегов Колумбии, юж. часть Дарьенского залива. Длина 87
км.Глубины 25–54
м.В У. впадает река Атрато. Порт Турбо.
Урава
Ура'ва,город в Японии, на о. Хонсю. Административный центр префектуры Сайтама. Город-спутник
.324 тыс. жителей (1974). Металлообработка и машиностроение; химическая, текстильная промышленность. Университет.
Уравнение
Уравне'ниев математике, аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых значения функций равны, – решениями (корнями); о таких значениях неизвестных говорят, что они удовлетворяют данному У. Например, 3
x –6
=0 является У. с одним неизвестным, а
х= 2 есть его решение;
x
2+
y
2
=25 является У. с двумя неизвестными, а
х =3
,
y= 4 есть одно из его решений. Совокупность решений данного У. зависит от области
Мзначений, допускаемых для неизвестных. У. может не иметь решений в
М,тогда оно называется неразрешимым в области
М.Если У. разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Например, У.
x
4
–4
=0 неразрешимо в области рациональных чисел, но имеет два решения:
x
1
=
, x
2
= –
в области действительных чисел и четыре решения:
x
1
=
, x
2
= –
, x
3
= i
, x
4
= –
в области комплексных чисел. У. sin
x= 0 имеет бесконечное множество решений:
x
k
= kp (
k =0, ± 1, ± 2,...) в области действительных чисел. Если У. имеет решениями все числа области
М,то оно называется тождеством в области
М.Например, У.
х =
является тождеством в области неотрицательных чисел и не является тождеством в области действительных чисел. Совокупность У., для которых требуется найти значения неизвестных, удовлетворяющие одновременно всем этим У., называется системой У.; значения неизвестных, удовлетворяющих одновременно всем У. системы, – решениями системы. Например,
х +2
y =5
,2
x + у – z= 1
является системой двух У. с тремя неизвестными; одним из решений этой системы является
х =1
, у =2
, z =3. Две системы У. (или два У.) называются равносильными, если каждое решение одной системы (одного У.) является решением др. системы (другого У.), и наоборот, причём обе системы (оба У.) рассматриваются в одной и той же области (см.
)
.Например, У.
х– 4 = 0 и 2
x– 8 = 0 равносильны, т.к. решением обоих У. является лишь
х =4. Всякая система У. равносильна системе вида
f
k(
x
1
, x
2
,..., х
п)
= 0, где
k =1, 2,...
Процесс разыскания решений У. заключается обычно в замене У. равносильным. В некоторых случаях приходится заменять данное У. другим, для которого совокупность решений шире, чем у данного У. Решения нового У., не являющиеся решениями данного У., называются посторонними решениями (см.
)
. Например, возводя в квадрат У.
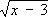 , получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У. Наиболее изучены У., для которых функции
f
kявляются многочленами от переменных
x
1
, x
2
,..., х
п
, –алгебраические У. Например, алгебраическое У. с одним неизвестным имеет вид:
a
0
x
n
+ a
1
x
n-1
+... + a
n= 0
(
a
0¹ 0); (*) число
nназывается степенью У. Решение алгебраич. У. было одной из важнейших задач алгебры в 16–17 вв., когда были получены формулы и методы решения алгебраических У. 3-й и 4-й степеней (см.
,
) (правила решения алгебраических У. 1-й и 2-й степеней были известны ещё в глубокой древности). Для корней У. 5-й и высших степеней общей формулы не существует, поскольку эти У., вообще говоря, не могут быть решены в радикалах (Н.
,1824). Вопрос о разрешимости алгебраических У. в радикалах привёл (около 1830) Э.
к общей теории алгебраических У. (см.
)
. Каждое алгебраическое У. всегда имеет хотя бы одно решение, действительное или комплексное. Это составляет содержание т. н. основной теоремы алгебры, строгое доказательство которой впервые было дано К.
в 1799. Если a – решение У. (*), то многочлен
a
0
x
n
+ a
1
x
n-1
+... + a
n
делится на
х –a
.Если он делится на (
х –a)
k
,но не делится на (
х –a)
k+1, то решение a имеет кратность
k.Число всех решений У. (*), если каждое считать столько раз, какова его кратность, равно
n. Если
f(
x)
–
,то У.
f(
x)
=0 называются трансцендентным (см., например,
)
,причём в зависимости от вида
f(
x) оно называется тригонометрическим У., логарифмическим У., показательным У. Рассматриваются также иррациональные У., то есть У., содержащие неизвестное под знаком радикала. При практическом решении У. обычно применяются различные приближённые методы решения У. Среди систем У. простейшими являются системы линейных У., то есть У., в которых
f
kсуть многочлены первых степеней относительно
x
1
, x
2
,..., х
п(см.
)
. Решение системы У. (не обязательно линейных) сводится, вообще говоря, к решению одного У. при помощи т. н. исключения неизвестных (см. также
)
. В аналитической геометрии одно У. с двумя неизвестными интерпретируется при помощи кривой на плоскости, координаты всех точек которой удовлетворяют данному У. Одно У. с тремя неизвестными интерпретируется при помощи поверхности в трёхмерном пространстве. При этой интерпретации решение системы У. совпадает с задачей о разыскании точек пересечения линий, поверхностей и т.д. У. с большим числом неизвестных интерпретируются при помощи многообразий в
n-мерных пространствах. В теории чисел рассматриваются неопределенные У., то есть У. с несколькими неизвестными, для которых ищутся целые или же рациональные решения (см.
)
.Например, целые решения У.
x
2
+ y
2
= z
2
вид
х = m
2
-n
2
, у =2
mn, z = m
2
+ n
2
где
mи
n –целые числа. С наиболее общей точки зрения, У. является записью задачи о разыскании таких элементов некоторого множества
А,что
F(
a)
= Ф(
а), где
Fи Ф – заданные
множества
Ав множество
В.Если множества
Аи
Вявляются множествами чисел, то возникают У. рассмотренного выше вида. Если
Аи
В– множества точек в многомерных пространствах, то получаются системы У., если же
Aи
В– множества функций, то в зависимости от характера отображения могут получаться также
,
и др. виды У. Наряду с вопросами нахождения решения У. в общей теории У. различного вида изучаются вопросы существования и единственности решения, непрерывной зависимости его от тех или иных данных и т.д. Термин «У.» употребляется (в отличном от указанного выше смысле) и в др. естественных науках, см., например,
(в астрономии),
(в физике),
,
в электродинамике,
в теории газов.
Уравнение времени
Уравне'ние вре'мени,разность между средним и истинным солнечным временем; равна разности прямых восхождений истинного и среднего Солнца. Часто У. в. определяют как разность истинного и среднего времени; в этом случае оно имеет противоположный знак, что нужно иметь в виду при пользовании справочниками. У. в. непрерывно меняется. Это обусловлено тем, что истинное солнечное время, измеряемое часовым углом истинного Солнца, течёт неравномерно вследствие, во-первых, неравномерности движения Земли по орбите и, во-вторых, наклона эклиптики к экватору. Поэтому У. в. получается в результате сложения двух волн приблизительно синусоидальной формы и почти равной амплитуды (см.
рис.
). Одна из этих волн имеет годичный, другая – полугодичный периоды. Четыре раза в году, а именно: около 16 апреля, 14 июня, 1 сентября и 25 декабря У. в. равно нулю и достигает 4 раза наибольшего значения (по абсолютной величине): около 12 февраля + 14,3
мин,15 мая – 3,8
мин,27 июля + 6,4
мини 4 ноября – 16,4
мин.С помощью У. в. может быть найдено среднее местное солнечное время, если известно истинное солнечное время, определённое по наблюдениям Солнца, например с помощью солнечных часов; при этом пользуются формулой:
m = m
0+ h
, где
m –среднее время,
m
0
–истинное время, h – У. в. Значения У. в. на каждый день даются в астрономических ежегодниках и календарях. См.
. График уравнения времени: 1 — составляющая уравнения времени, определяемая неравномерностью движения Земли по орбите; 2 — составляющая уравнения времени, определяемая наклоном эклиптики к экватору; 3 — уравнение времени.
Уравнение состояния
Уравне'ние состоя'ния,связывает давление
р,объём
Vи температуру Т физически однородной системы в состоянии
: f(
p, V, Т)
=0. Это уравнение называется термическим У. с., в отличие от калорического У. с., определяющего
системы
Uкак функцию какого-либо двух из трёх параметров
р, V, Т.Термическое У. с. позволяет выразить давление через объём и температуру
р = p(
V, Т) и определить элементарную работу d
A= =
pd
Vпри бесконечно малом расширении системы d
V. У. с. является необходимым дополнением к термодинамическим законам, которое делает возможным их применение к реальным веществам. Оно не может быть выведено с помощью одних только законов
,а определяется или рассчитывается теоретически на основе представлений о строении вещества методами
.Из
следует лишь существование калорического У. с., а из
– связь между термическим и калорическим У. с.
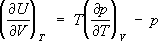 ,
,откуда вытекает, что для
внутренняя энергия не зависит от объёма
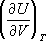 = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
ввиде функции своих параметров. Например, если известна
Fкак функция
Ти
V,то У. с. находят дифференцированием:
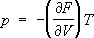 ,
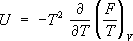 . Примерами У. с. для газов может служить
для идеального газа
pu
= RT,где
R –
,u
–объём 1
молягаза;
,где
аи
b– постоянные, зависящие от природы газа и учитывающие влияние сил притяжения между молекулами и конечность из объёма, вириальное У. с. для неидеального pu / RT = 1 + B (
T)
/u
+С (
Т)/ u
2
+.., где
В(
Т)
, С(
Т)
... –2-й, 3-й и т.д. вириальные коэффициенты, зависящие от сил взаимодействия между молекулами (см.
)
.Это уравнение является наиболее надёжным и теоретически обоснованным У. с. для газов и позволяет объяснить многочисленные экспериментальные результаты на основании простых моделей
.Были предложены также различные эмпирические У. с., основанные на экспериментальных данных о теплоёмкости и сжимаемости. У. с. неидеальных газов указывает на существование критической точки (с параметрами
p
k
, V
k
, T
k)
,в которой газообразная и жидкая фазы становятся идентичными (см.
)
.Если У. с. представить в виде приведенного У. с., т. е. в безразмерных переменных
p/p
k
, V/V
k
, T/T
k
,то при не слишком низких температурах это уравнение мало меняется для различных веществ (закон
)
. Для равновесного излучения, или фотонного газа, У. с. определяется
для средней плотности энергии. Для жидкостей из-за сложности учёта всех особенностей взаимодействия молекул пока не удалось теоретически получить общее У. с. Уравнение Ван-дер-Ваальса хотя и применяют для качественной оценки поведения жидкостей, но оно по существу неприменимо ниже критической точки, когда возможно сосуществование жидкой и газообразной фаз. У. с., хорошо описывающее свойства ряда простых жидкостей, можно получить из приближённых теорий жидкого состояния типа теории свободного объёма или дырочной теории (см.
)
.Знание распределения вероятности взаимного расположения молекул (парной корреляционной функции) принципиально позволяет вычислить У. с. жидкости, но эта задача очень сложна и полностью ещё не решена даже с помощью вычислительных машин. Для твёрдых тел термическое У. с. определяет зависимость
от температуры и давления. Оно может быть получено на основании теории теплового движения в кристаллах, рассматривающей
и их взаимодействие, но пока общего У. с. для твёрдых тел не найдено. Для магнитных сред элементарная работа при намагничивании равна d
A= -
Нd
М,где
М– магнитный момент,
Н –напряжённость магнитного поля. Следовательно, зависимость
М = М(
Н, Т) представляет собой магнитное У. с. Для электрически поляризуемых сред элементарная работа при поляризации равна d
A= -
Еd
Ргде
Р -поляризация,
Е -напряжённость электрического поля, следовательно, У. с. имеет вид
Р= (
Е, Т)
.
Лит.:Хилл Т., Статистическая механика, пер. с англ., М., 1960; Вукалович М. П., Новиков И. И., Уравнение состояния реальных газов, М. – Л., 1948; Мейсон Э., Сперлинг Т., Вириальное уравнение состояния, пер. с англ., М., 1972; Лейбфрид Г., Людвиг В., Теория ангармонических эффектов в кристаллах, пер. с англ., М., 1963. См. также лит. при статьях
и
.
Д. Н. Зубарев.
Уравнения математической физики
Уравне'ния математи'ческой фи'зики,дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У. м. ф. с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование (см.
).
Классификация уравнений математической физики.Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:
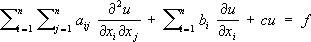 , (1) где все коэффициенты
a
ij(
a
ij
= a
ij)
, b
i
, си правая часть
fпредставляют собой заданные функции независимых переменных
x
1
, x
2
,..., х
п(
n³ 2)
,а
u –искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно l) уравнения
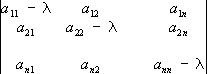 = 0, (2) и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все
nкорней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных
n –1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты
a
ijпостоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от
x
1
,..., х
п
,то и корни уравнения (2) зависят от
x
1
,..., х
п
,а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими). Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.
Основные примеры уравнений математической физики.
:
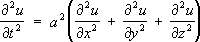 – простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) –
и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.
:
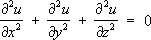 – простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение –
.Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний.
:
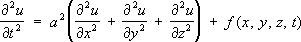 – простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания. Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:
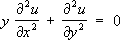 Для этого уравнения полуплоскость
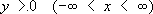 служит зоной эллиптичности, полуплоскость
у< 0 – зоной гиперболичности, а прямая
у= 0 – зоной параболичности. Ряд задач математической физики приводит к
различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое
. Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д'Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л.
(1770), П.
предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см.
,
). Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см.
.
)
.При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.
Лит.:Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Годунове. К., Уравнения математической физики, М., 1971; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.
Уравнения химические
Уравне'ния хими'ческие,изображения
посредством
,
,чисел и математических знаков. На возможность такого описания химических реакций указал в 1789 А.
,основываясь на
;однако всеобщее применение У. х. получили только в 1-й половине 19 в. Каждое У. х. состоит из двух частей – левой и правой, соединённых знаком равенства (иногда для обозначения направления реакции – простой стрелкой ®, а реакции обратимой – двойной
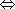 .
.). В левой части пишут формулы исходных веществ, в правой – формулы полученных веществ; между формулами ставят знак +. При составлении У. х. принимают, что масса полученных веществ равна массе исходных и что число атомов одних и тех же элементов должно быть в обеих частях У. х. одинаковым. Перед формулами исходных и полученных веществ ставят коэффициенты, которые должны быть целыми числами. Например, зная, что при горении метана в кислороде образуются вода и двуокись углерода, можно сразу написать У. х. этой реакции: CH
4+ 2O
2= 2H
2O + CO
2. (1) В более сложных случаях применяют приёмы, описанные в ст.
,а также способ, основанный на решении систем неопределённых уравнений. Например, требуется подобрать коэффициент У. х. обжига пирита FeS
2в кислороде:
xFeS
2+
yO
2= 2Fe
2O
3+
tSO
2. (2) Очевидно, что
х =2
z, t =2
x, 1y = 3z + 2t.Положив
z= 1, имеем:
х= 2,
t= 4,
у= 5,5. Умножив эти числа на 2, получаем: 4FeS
2+ 11O
2= 2Fe
2O
3+ 8SO
2. На основании У. х. делаются расчёты, необходимые в лабораторной и заводской практике.
Лит.:Некрасов Б. В., Основы общей химии, 3 изд., т. 1, М., 1973.
С. А. Погодин.
Уравнивающие импульсы
Ура'внивающие и'мпульсыв телевидении, узкие импульсы, расположенные на кадровом гасящем импульсе полного
(до и после кадрового синхронизирующего импульса – КСИ). У. и. вводят в состав сигнала синхронизации при
в целях устранения различия в форме чётных и нечётных КСИ, которое появляется при выделении последних из сигнала синхронизации (интегрирующим фильтром) вследствие неодинакового расположения в них строчных синхронизирующих импульсов. Длительность У. и. ~2,5
мксек;частота следования равна двойной строчной частоте. Количество У. и. определяется требованиями по идентичности чётных и нечётных КСИ и обычно равно 5–6.
Лит.см. при ст.
.
Уравнительные вычисления
Уравни'тельные вычисле'нияв геодезии, совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений. У. в. проводятся для устранения противоречий (невязок), обусловленных наличием ошибок в избыточно измеренных величинах, и для определения вероятнейших значений искомых неизвестных или их значений, близких к вероятнейшим. В процессе У. в. это достигается путём определения поправок к измеренным величинам (углам, направлениям, длинам линий или превышениям). Обычно поправки определяют с помощью
так, чтобы сумма квадратов всех поправок была наименьшей. В этом случае вычисления называют строгими и неизвестные (поправки), определяемые из такого рода У. в., имеют вероятнейшие значения.
Так, в простейшем примере плоского треугольника сумма углов должна строго равняться 180°. Измеренные углы вследствие ошибок измерения этому условию, вообще говоря, не удовлетворяют и должны быть исправлены прибавлением соответствующих поправок. Из всего бесконечного множества поправок, которые приводят сумму измеренных углов к 180°, лишь одна система поправок обладает тем свойством, что сумма квадратов их есть минимум; такая система считается вероятнейшей. В приведённом примере это имеет место, если невязку разложить поровну на все три угла.
Однако применение способа наименьших квадратов к уравниванию измеренных величин вполне законно только в том случае, когда ошибки их имеют случайный характер. Строгое уравнивание геодезических сетей, особенно больших по размерам, сопряжено с рядом трудностей технического и организационного характера. Поэтому на практике часто применяются различные упрощённые способы У. в. В геодезической практике как при строгом, так и при упрощённых У. в. широко используются главным образом два способа уравнивания: способ условных измерений и способ посредственных измерений. При первом способе поправки отыскивают непосредственно к измеренным величинам, при втором – к их функциям (как правило, координатам).
Всякий способ уравнивания состоит из следующих основных процессов: предварительных (подготовительных) вычислений, составления условных уравнений или уравнений погрешностей, составления нормальных уравнений, решения нормальных уравнений и оценки точности измеренных и уравненных величин. При большом числе нормальных уравнений наиболее трудоёмкой частью У. в. является их решение, поэтому оно обычно осуществляется на ЭВМ. Уравнения могут решаться методом последовательного исключения неизвестных (схема Гаусса) или методом итерации (приближений). Иногда нормальные уравнения не составляют; в этом случае неизвестные определяют непосредственно из решения или условных уравнений, или уравнений погрешностей. В некоторых случаях при обработке материалов геодезических измерений невысокой точности уравнивание результатов выполняют графическим способом.
Уравнительный резервуар ГЭС
Уравни'тельный резервуа'р ГЭС,ёмкость, расположенная в конце напорной
перед турбинными напорными трубопроводами; обычно выполняется в виде цилиндра с открытым верхним торцом. У. р. улучшает условия регулирования мощности гидротурбин и предохраняет деривацию от гидравлического удара, возникающего при внезапном закрытии направляющего аппарата в случае сброса нагрузки или в результате аварии.
Страницы:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
|
|


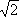
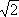
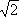
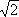
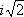
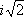
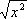
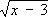 , получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.
, получают У.
x- 3 = 4, решение которого
х= 7 является посторонним для исходного У. Поэтому, если при решении У. делались действия, могущие привести к появлению посторонних решений (например, возведение У. в квадрат), то все полученные решения преобразованного У. проверяют подстановкой в исходное У.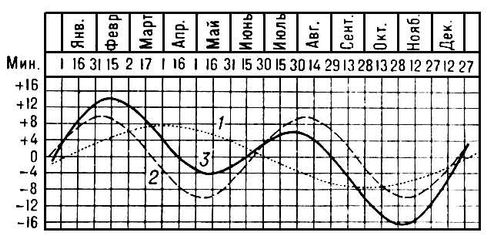
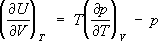 ,откуда вытекает, что для
внутренняя энергия не зависит от объёма
,откуда вытекает, что для
внутренняя энергия не зависит от объёма
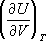 = 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
ввиде функции своих параметров. Например, если известна
Fкак функция
Ти
V,то У. с. находят дифференцированием:
= 0. Термодинамика показывает, что для вычисления как термического, так и калорического У. с., достаточно знать любой из
ввиде функции своих параметров. Например, если известна
Fкак функция
Ти
V,то У. с. находят дифференцированием: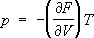 ,
,
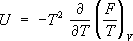 .
.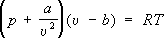
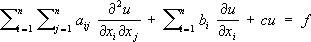 , (1)
, (1)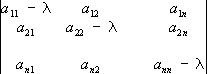 = 0, (2)
= 0, (2)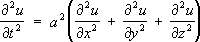
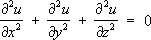
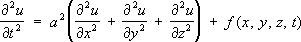
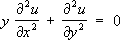
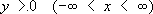 служит зоной эллиптичности, полуплоскость
у< 0 – зоной гиперболичности, а прямая
у= 0 – зоной параболичности.
служит зоной эллиптичности, полуплоскость
у< 0 – зоной гиперболичности, а прямая
у= 0 – зоной параболичности.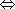 .). В левой части пишут формулы исходных веществ, в правой – формулы полученных веществ; между формулами ставят знак +. При составлении У. х. принимают, что масса полученных веществ равна массе исходных и что число атомов одних и тех же элементов должно быть в обеих частях У. х. одинаковым. Перед формулами исходных и полученных веществ ставят коэффициенты, которые должны быть целыми числами. Например, зная, что при горении метана в кислороде образуются вода и двуокись углерода, можно сразу написать У. х. этой реакции:
.). В левой части пишут формулы исходных веществ, в правой – формулы полученных веществ; между формулами ставят знак +. При составлении У. х. принимают, что масса полученных веществ равна массе исходных и что число атомов одних и тех же элементов должно быть в обеих частях У. х. одинаковым. Перед формулами исходных и полученных веществ ставят коэффициенты, которые должны быть целыми числами. Например, зная, что при горении метана в кислороде образуются вода и двуокись углерода, можно сразу написать У. х. этой реакции: