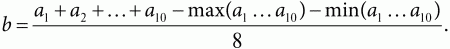Новая и чрезвычайно интересная форма внеклассной работы по предмету. Учителя, знающие, как устроены лиги в чемпионатах страны по различным видам спорта, без труда разберутся в этой системе.
Принцип проведения игры прост. Сначала дается общее задание для всех, по результатам которого определяется, кто в какой лиге (второй, первой, высшей или суперлиге) начинает играть.
Далее выбирается день недели, в который постоянно будут проходить соревнования. Выбор дня определяется действующим расписанием. Желательно, чтобы все классы параллели имели одинаковое количество уроков в этот день (напоминаем, что в олимпиаде участвуют все).
Для лучшего понимания рассмотрим правила игры на конкретном примере.
Пусть в параллели пятых классов 53 человека. После предварительного тура 10 человек определены в суперлигу, 15 – в высшую, 15 – в первую и 13 – во вторую. Определен постоянный день игр – четверг.
В первый такой четверг соревнуются участники второй лиги (вторая лига, 1 тур). Они решают шесть заданий за 40–60 мин (время определяется учителем). После проведения первого тура и проверки работ участники, занявшие первые пять мест, переходят в первую лигу. Остальные 8 человек получают места с 53 по 46.
В следующий четверг соревнуются 20 человек (15 человек, определенных первоначально в первую лигу плюс пятеро перешедших из второй лиги). После проверки работ происходит следующее: лучшие 5 участников переходят в высшую лигу; остальные 15 человек получают места с 45 по 31; 5 участников, занявших последние места (в нашем примере 41–45 места), переходят во вторую лигу.
В следующий (третий) четверг соревнуются 20 человек (15 человек, определенных изначально в высшую лигу плюс пятеро перешедших из первой лиги). После проверки работ, как и в предыдущем случае: 5 лучших участников переходят в суперлигу; остальные 15 человек получают места с 30 по 16; 5 участников, занявших 26–30 места, переходят в первую лигу.
В четвертый четверг проходит первый тур суперлиги. Все участники в итоге получают места с 1 по 15, причем участники, занявшие 11–15 места, переходят в высшую лигу.
Затем по тем же правилам проходит второй тур в каждой из четырех лиг, затем третий и т. д.
Если учащийся по болезни или по другим причинам пропускает какой-нибудь тур своей лиги, то он набирает 0 баллов и выбывает в более низшую лигу (а если он во второй лиге – просто занимает последнее место).
В книге представлено два комплекса олимпиад по лигам:
1. Олимпиады по лигам (5–6 классы), адаптированные под учебник Г. В. Дорофеева и Л. Г. Петерсон. Учителя математики знают, что если пятиклассники учатся по учебному комплекту Г. В. Дорофеева и Л. Г. Петерсон, то за 5 класс проходится чуть ли не вся программа 6 класса. Это нашло свое отражение в содержании задач.
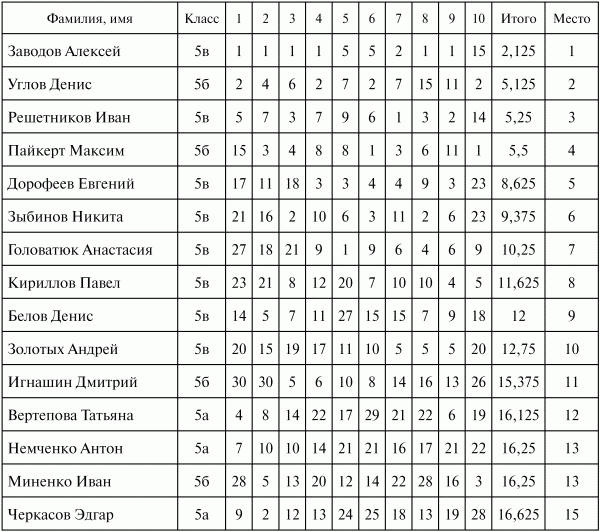
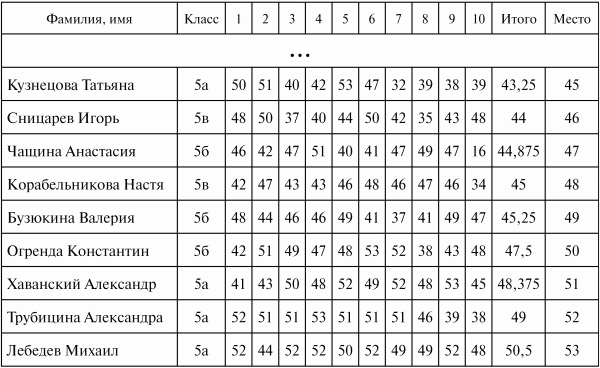
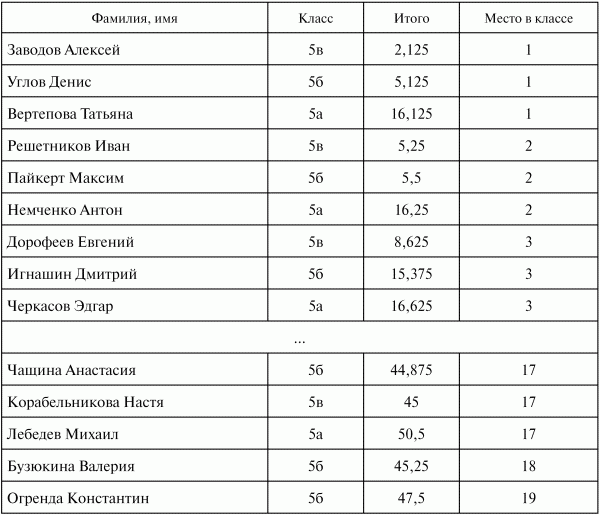
Всего в лигах предусмотрено 10 туров. Итоговые результаты подводятся просто (лучше всего это сделать в Excel). Пусть некоторый учащийся в течение десяти туров занимал места: ах, а2, ах... а. Из данных чисел отбрасываются лучший и худший результаты, а далее считается среднее арифметическое оставшихся 8 чисел:
У кого меньше число Ь, тот и выиграл (для сортировки участников по местам можно применить известную в Excel команду РАНГ). Небольшое пояснение: лучший результат отбрасывается, так как бывает случайное попадание учащегося в высшую лигу и суперлигу перед первым туром, а худший результат учащийся также может показать случайно, например, вследствие пропуска по болезни.
Итоговая таблица может выглядеть так:
2. Олимпиады по лигам (5–6 классы), адаптированные под учебник Н. Я. Виленкина и др.
Эти олимпиады четко разделены на два вида:
стандартная лига (примеры, уравнения, типовые задачи и т. д.);
олимпиадная лига (нестандартные задания).
Разделение связано с тем, что в учебном комплекте Н. Я. Виленкина и др. практически отсутствуют задачи на развитие логического мышления (правда, это не является недостатком учебника, просто он преследует другие дидактические цели). А потому есть смысл разделить математическое соревнование учащихся на две части.
Итоги подводятся так же, как и при проведении олимпиад, адаптированных под учебник Г. В. Дорофеева и Л. Г. Петерсон. Те же 10 туров, та же формула для подведения итогов.
Практика показала, что детям очень нравится такое соревнование. Неожиданным и одновременно приятным было то обстоятельство, что учащиеся, занимающие последние места, рвались на игру не хуже «обитателей суперлиги» и также живо обсуждали каждый промежуточный итог игры.
Выражаю большую благодарность своим коллегам: Наталье Михайловне Дорофеевой и Ольге Алексеевне Коржовой, которые вместе с автором книги разработали данную форму проведения математических олимпиад.