 |
|
Популярные авторы:: БСЭ :: Андерсон Пол Уильям :: Толстой Лев Николаевич :: Говард Роберт Ирвин :: Биленкин Дмитрий Александрович :: Желязны Роджер :: Андреев Леонид Николаевич :: Лесков Николай Семёнович :: Дансени Лорд :: Чапек Карел Популярные книги:: Справочник по реестру Windows XP :: Пичугин мост :: Бурый волк :: Маски :: Затишье :: Падение Эдварда Барнарда :: Мясоеды :: Подозрение :: Чайная роза :: Шакир |
Большая Советская Энциклопедия (ОБ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ОБ) - Чтение (стр. 16)
В области температур от
Т
кдо
Т
тпри изотермическом снижении давления, например по
изотерме
cd, из однородной газовой фазы выпадают капли жидкости (в точке
с), количество жидкости постепенно увеличивается до максимального значения в точке
F, а затем начинает снижаться, и в точке
dжидкая фаза исчезает полностью (т. н. изотермическая О. к. или О. к. первого рода). Зона
KMG, в которой происходит аномальное выделение конденсата при снижении
р, называется областью О. к. (слово «обратная» указывает на возвращение системы вновь в двухфазное состояние). Широкое практическое применение явление изотермической О. к. получило при добыче
конденсата газового
из газоконденсатных месторождений природного газа.
При пересечении двухфазной области по адиабате в интервале давлений от р кдо р т, например по линии ab, в однородной жидкой смеси появляются пузырьки газа (в точке а), количество газа с ростом Тсначала увеличивается, а затем убывает и в точке bсистема вновь становится жидкой (т. н. обратное испарение или О. к. второго рода). Лит.:Карапетьянц М. Х., Химическая термодинамика, 2 изд., М. - Л., 1953, с. 317-18; Руководство по добыче, транспортировке и переработке природного газа, [М.], 1965, с. 75-76. Б. В. Дегтярев. 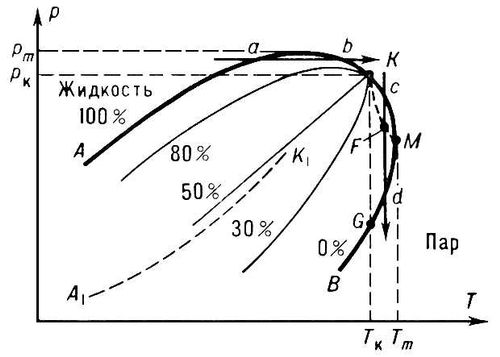
Фазовая диаграмма двухкомпонентной системы постоянного состава вблизи критической точки К жидкость - пар ( Т- температура, p- давление). Обратная лопата Обра'тная лопа'та, см. в ст. Механическая лопата . Обратная матрица
Обра'тная ма'трицадля данной квадратной
матрицы
А =
Обратная связь Обра'тная связь, обратное воздействие результатов процесса на его протекание или управляемого процесса на управляющий орган. О. с. характеризует системы регулирования и управления в живой природе, обществе и технике. Различают положительную и отрицательную О. с. Если результаты процесса усиливают его, то О. с. является положительной. Когда результаты процесса ослабляют его действие, то имеет место отрицательная О. с. Отрицательная О. с. стабилизирует протекание процессов. Положительная О. с., напротив, обычно приводит к ускоренному развитию процессов и к колебательным процессам, В сложных системах (например, в социальных, биологических) определение типов О. с. затруднительно, а иногда и невозможно. О. с. классифицируют также в соответствии с природой тел и сред, посредством которых они осуществляются: механическая (например, отрицательная О. с., осуществляемая центробежным регулятором Уатта в паровой машине); оптическая (например, положительная О. с., осуществляемая оптическим резонатором в лазере ); электрическая и т.д. Иногда О. с. в сложных системах рассматривают как передачу информации о протекании процесса, на основе которой вырабатывается то или иное управляющее воздействие. В этом случае О. с. называют информационной. Понятие О. с. как формы взаимодействия играет важную роль в анализе функционирования и развития сложных систем управления в живой природе и обществе, в раскрытии структуры материального единства мира. Л. И. Фрейдин. Обратная связь в системах автоматического регулирования и управления,связь в направлении от выхода к входу рассматриваемого участка основной цепи воздействий (передачи информации). Этим участком может быть как управляемый объект, так и любое звено автоматической системы (либо совокупность звеньев). Основная цепь воздействий - условно выделяемая цепь прохождения сигналов от входа к выходу автоматической системы. О. с. образует путь передачи воздействий в дополнение к основной цепи воздействий или какому-либо её участку. Благодаря О. с. результаты функционирования автоматические системы воздействуют на вход этой же системы или, соответственно, её части, влияют на характер их функционирования и математическое описание движения. Такие системы с замкнутой цепью воздействий - замкнутые системы управления - характеризуются тем, что для них входными являются как внешние, так и контрольные воздействия, т. е. идущие от управляемого объекта на управляющее устройство. Цепь (канал) О. с. может содержать одно или несколько звеньев, осуществляющих преобразование выходного сигнала основной цепи воздействий по заданному алгоритму . Пример цепи О. с. - управляющее устройство (например, автоматический регулятор), получающее в качестве входной величины выходное (действительное) воздействие управляемого объекта и сравнивающее его с предписанным (в соответствии с алгоритмом функционирования) значением. В итоге этого сравнения формируется воздействие управляющего устройства на управляемый объект (см. Регулирование автоматическое ). Т. о., объект управления охватывается цепью О. с. в виде управляющего устройства, цепь воздействия замыкается; такая О. с. называется обычно главной. О. с. является фундаментальным понятием кибернетики , особенно теории управления и теории информации; О. с. позволяет контролировать и учитывать действительное состояние управляемой системы (т. е., в конечном счёте, результаты работы управляющей системы) и вносить соответствующие корректировки в её алгоритм управления. В технических системах контрольная информация о работе управляемого объекта поступает по цепи О. с. к оператору или автоматическому управляющему устройству. Отрицательная О. с. широко используется в замкнутых автоматических системах с целью повышения устойчивости (стабилизации), улучшения переходных процессов, понижения чувствительности и т.п. (под чувствительностью понимается отношение бесконечно малого изменения выходного воздействия к вызвавшему его бесконечно малому входному воздействию). Положительная О. с. усиливает выходное воздействие звена (или системы), приводит к повышению чувствительности и, как правило, к понижению устойчивости (часто к незатухающим и расходящимся колебаниям), ухудшению переходных процессов и динамических свойств и т.п. По виду преобразования воздействия в цепи О. с. различают жёсткую (статическую), дифференцирующую (гибкую, упругую) и интегрирующую О. с. Жёсткая О. с. содержит только пропорциональные звенья и её выходное воздействие пропорционально входному (как в статике, так и в динамике - в определённом диапазоне частот колебаний). Дифференцирующие связи содержат дифференцирующие звенья (простые, изодромные) и могут быть астатическими (исчезающими со временем) или со статизмом. Связи без статизма проявляются только в динамике, так как в их математической модели не участвует входное воздействие, а фигурируют лишь его производные, стремящиеся к нулю с окончанием переходных процессов. В состав интегрирующей О. с. входит интегрирующее звено, накапливающее со временем поступающие воздействия. Для систем с О. с. справедливы следующие закономерности. Пропорциональное звено при охвате О. с. остаётся пропорциональным с новым коэффициентом передачи, увеличенным (против исходного) при положительной и уменьшенным при отрицательной О. с. Статическое звено первого порядка при охвате жёсткой отрицательной О. с. остаётся статическим первого порядка; меняются постоянная времени и коэффициент передачи. Интегрирующее звено при охвате жёсткой отрицательной О. с. превращается в статическое, а при охвате изодромной О. с. начинает реагировать и на производную (по времени) входного воздействия. Статическое звено первого порядка при охвате изодромной О. с. также реагирует и на производную (по времени) входного воздействия. При охвате пропорционального звена интегрирующей отрицательной О. с. получается инерционно-дифференцирующее звено. Если при этом исходное пропорциональное звено имеет весьма большой коэффициент передачи (по сравнению с коэффициентом передачи изодромной О. с.), то образующееся звено приближается по своей характеристике к дифференцирующему. Лит.:Хэммонд П. Х., Теория обратной связи и её применения, пер. с англ., М., 1961; Винер Н., Кибернетика, пер. с англ., М., 1958; его же, Кибернетика и общество, пер. с англ., М., 1958; Теория автоматического управления, ч. 1-2, М., 1968-72; Основы автоматического управления, 3 изд., М., 1974. М. М. Майзель. Обратная связь в радиоэлектронных устройствах,воздействие сигнала с выхода устройства на его вход. Электрическая цепь, по которой сигнал с выхода устройства подаётся на вход, называется цепью О. с. Чаще всего устройство можно представить в виде эквивалентной электрической цепи, имеющей две (входную и выходную) пары зажимов, и характеризовать т. н. передаточной функцией, или функцией передачи, определяемой отношением напряжения или тока на выходной паре зажимов к напряжению или току на входной паре зажимов. Функция передачи F cустройства с О. с. может быть определена из формулы:
где F 0- функция передачи устройства без О. с.; b- функция цепи О. с.; bF 0- петлевое усиление; 1 - bF 0- глубина О. с. Классификация О. с.О. с. классифицируют главным образом по виду функции передачи цепи О. с. и соотношению функций передачи цепи О. с. и самого устройства, по характеру цепи О. с., по способу подключения цепи О. с. ко входу и выходу устройства. Различают линейную и нелинейную О. с. в зависимости от того, линейна или нелинейна функция передачи цепи О. с. Если bF 0- действительное число и > 0, О. с. является положительной; если bF 0- действительное число и < 0, О. с. является отрицательной. При гармоническом входном колебании характер и глубина О. с. могут оказаться различными при разных частотах этого колебания. Такую О. с. называют частотно-зависимой. Она может быть положительной при одной частоте, когда фазы колебаний, которые подаются на вход устройства с выхода цепи О. с. и извне, совпадают (разность фаз Dj = 0°), и отрицательной при др. частоте, когда они противоположны. При частоте, на которой Dj не равна 0° или 180°, функция передачи цепи О. с. представляет собой комплексное число ; такая О. с. называют комплексной. При Dj, равной 90°, О. с. называют иногда (чисто) реактивной. Если цепь комплексной О. с. содержит линию задержки , т. е. если Dj приблизительно пропорциональна частоте колебаний, О. с. называется запаздывающей. Если О. с. осуществляют подключением к устройству дополнительных цепей, то она называется внешней; если О. с. обусловливается физическими явлениями в самих электронных приборах, используемых в устройстве, то она называется внутренней. Если внешняя цепь О. с. возникла непреднамеренно. то О. с. называется паразитной. По способу подключения цепей О. с. ко входу и выходу устройства различают последовательную и параллельную О. с., если выход цепи О. с. подключен последовательно ( рис. 1 , а, б) или параллельно ( рис. 1 , б, г) источнику сигнала, и смешанную (комбинированную) по входу, если подключение цепей О. с. к источнику сигнала последовательно-параллельное. Различают также О. с. по напряжению и по току, если напряжение или ток на входе цепи О. с. пропорциональны соответственно напряжению на нагрузочном сопротивлении ( рис. 1 , б, г) или току в нём ( рис. 1 , а, в), и О. с. смешанную (комбинированную) по выходу, если подключение цепей О. с. к нагрузочному (выходному) сопротивлению последовательно-параллельное. О. с., при которой с выхода на вход устройства передаются только помехи и искажения сигнала, возникающие в устройстве, наз. балансной. Свойства и применение обратной связи.В устройстве с положительной О. с. при петлевом усилении e 1 могут возникнуть автоколебания, что и используют в различного рода генераторах электрических колебаний. Положительные О. с. с bF 0< 1 применяют для усиления некоторых свойств устройства, например для увеличения селективности и чувствительности радиоприёмника при регенеративном приёме. Важнейшим свойством отрицательной О. с. является то, что она приближает функцию передачи устройства к функции, обратной функции передачи цепи О. с., и тем сильнее, чем больше глубина О. с. Поэтому её применяют главным образом для стабилизации параметров устройства (например, коэффициент усиления усилителя электрических колебаний) и уменьшения возникающих в нём нелинейных искажений (в 1 - bF 0раз). Кроме функции передачи, О. с. изменяет входную и выходную реакции устройства с О. с. Отрицательная параллельная (последовательная) О. с. по напряжению (току) уменьшает (увеличивает) соответственно входное и выходное сопротивление устройства с О. с. Положительная О. с. ведёт себя противоположным образом. Комплексную частотно-зависимую О. с. применяют для создания т. н. активных электрических фильтров . Она также позволяет реализовать в электрических и радиотехнических устройствах элементы электрических цепей, не существующие в виде физических приборов, например элементы с отрицательной ёмкостью и с отрицательной индуктивностью, гиратор (преобразователь полного сопротивления, например ёмкостного в индуктивное) на любую рабочую частоту и элементы с электрически управляемыми параметрами (например, в виде реактивной лампы ). Иногда такая О. с. используется для нейтрализации нежелательной внутренней О. с. в электронных приборах. В одном устройстве нередко применяют одновременно несколько цепей О. с. различного характера. В качестве примера можно привести ламповый усилитель ( рис. 2 ) с комплексной частотно-зависимой параллельной О.с. по напряжению, реализуемой взаимной индуктивностью (т. н. трансформаторная О. с.), и отрицательной последовательной О. с. по току, осуществляемой резистором. На частоте, равной резонансной частоте колебательного контура, трансформаторная О. с. становится положительной. Если её петлевое усиление < 1 (с учётом действия отрицательной О. с), то всё устройство работает как регенеративный усилитель, в котором отрицательная О. с. стабилизирует глубину положит. О. с. и тем самым стабилизирует коэффициент усиления и полосу пропускания усилителя. Если же петлевое усиление e 1, то устройство работает как генератор электрических колебаний, в котором отрицательная О. с. ограничивает ток через электронную лампу и улучшает форму колебаний на выходе, приближая её к синусоидальной. Лит.:Брауде Г. В., Коррекция телевизионных и импульсных сигналов, Сб. ст., М., 1967; Цыкин Г. С., Усилительные устройства, 4 изд., М., 1971. Л. И. Фрейдин. Обратная связь в биологии.Существование систем регулирования с О. с. прослеживается на всех уровнях организации живого - от молекулярного до популяционного и биоценотического. Особенно значителен вклад этого механизма в автоматическое поддержание постоянства внутренних сред организма - гомеостаза , в деятельность генетического аппарата, эндокринной и нервной систем. Представления о регулировании по принципу О. с. появились в биологии давно. Уже первая гипотеза о рефлекторных реакциях (Р. Декарт , 17 в., Й. Прохаска , 18 в.) содержала предпосылки этого принципа. В более чёткой форме эти представления были развиты в работах Ч. Белла , И. М. Сеченова и И. П. Павлова , а позже - в 30-40-х гг. 20 в. Н. А. Бернштейном и П. К. Анохиным . В наиболее полном и близком к современному его пониманию виде принцип О. с. (отрицательной) - как общий принцип для всех живых систем - был сформулирован русским физиологом Н. А. Беловым (1912-24) под названием «параллельно-перекрестного взаимодействия» и экспериментально изучен на эндокринных органах М. М. Завадовским , назвавшим его «плюс - минус взаимодействием». Белов показал, что отрицательная О. с. - общий принцип, обеспечивающий тенденцию к равновесию в любых (не только живых) системах, но, как и Завадовский, считал, что в живых системах невозможно существование положительных О. с. Советским учёным А. А. Малиновским было показано наличие в живых системах всех типов О. с. и сформулированы различия их приспособительского значения (1945-60). За рубежом О. с. в биологии начали широко исследовать после появления в 1948 книги Н. Винера «Кибернетика». В СССР в 50-60-х гг. 20 в. И. И. Шмальгаузен успешно применил представление об О. с. в популяционной генетике. В живых системах следует различать О. с. типа взаимной стимуляции (положительная О. с.) или подавления в ответ на стимуляцию (отрицательная О. с.), поддающиеся хотя бы приближённой количественнной оценке, и качественно сложные О. с., когда, например в онтогенезе , один орган способствует дифференцировке другого, а последний, на новом этапе, определяет качественно развитие первого. Общие принципы О. с. сформулированы в основном для отношений первого типа. Отрицательная О. с. обеспечивает поддержание системы в устойчивом равновесии, т.к. увеличение воздействия управляющего органа на объект (регулируемый орган, систему, процесс) вызывает противоположное воздействие объекта на управляющий орган. Физиологический смысл отрицательной О. с. заключается в том, что увеличение регулируемой величины (например, активности органа) сверх некоего предела вызывает понижающее воздействие со стороны сопряжённой с нею подсистемы; резкое уменьшение регулируемой величины обусловливает противоположное воздействие. При положительной О. с. информация об увеличении регулируемой величины вызывает в связанной с нею подсистеме реакцию, обеспечивающую дальнейшее увеличение этой величины. У высокоорганизованных животных деятельность центральной нервной системы в норме всегда включает как необходимое условие наличие О. с. Так, любое действие животного, например погоня за добычей, сопровождается импульсами, поступающими от центральной нервной системы к мышцам (бег, схватывание добычи), и обратными сигналами от органов чувств (зрение, проприорецепторы и др.), позволяющими учитывать результаты усилий и корректировать их в связи с ходом событий. Саморегуляция процессов жизнедеятельности также обусловлена О. с. Так, подъём артериального давления выше нормы воспринимается специальными рецепторами (например, барорецепторами каротидного синуса ), которые сигнализируют об этом в вазомоторные центры нервной системы. Это приводит к возникновению центробежных импульсов, ведущих к снижению давления (см. Кровообращение ). Подобный процесс - пример отрицательной О. с., наиболее часто наблюдаемой в стабильных живых системах. Большинство регуляторных систем животных и растительных организмов работает по этому принципу. Положительная О. с. преобладают в период эмбрионального развития. Многие процессы в экологии, например регуляция динамики популяций, также основаны на положительной и отрицательной О. с. Так, особый случай отрицательной О. с. представляет собой рассмотренная итальянским математиком В. Вольтерра система хищник - жертва. Увеличение численности жертв способствует усиленному размножению хищников, а рост численности последних, напротив, - снижению численности жертв. Хотя таким образом равновесие и поддерживается в природе, по благодаря запозданию в размножении животных оно приобретает форму волн жизни - широких колебаний численности животных вокруг среднего уровня. На молекулярном уровне по принципу О. с. регулируется огромное число ферментативных реакций, одновременно протекающих в живой клетке. Координация этой сложной взаимосвязанной системы осуществляется путём изменения активности ферментов (отрицательную О. с. осуществляют ингибиторы, положительную - стимуляторы) или скорости их синтеза (О. с. осуществляют эффекторы; см. Оперон ). Комбинации положительных и отрицательных О. с. обусловливают альтернативную смену физиологических состояний (например, сон - бодрствование). Изучение кривой развития патологических процессов неинфекционного характера (трофические язвы, гипертония, маниакально-депрессивный психоз, эпилепсия и т.д.) позволяет, исходя из результата, определить наиболее вероятный тип О. с., лежащий в основе заболевания, и ограничить изучение его этиологии и патогенеза механизмами определённой категории. Живые объекты как наиболее совершенные саморегулирующиеся системы богаты различными типами О. с.; изучение последних - весьма продуктивно для исследования биологических явлений и установления их специфичности. Лит.:Малиновский А. А., Типы управляющих биологических систем и их приспособительное значение, в сборнике: Проблемы кибернетики, № 4, М., 1961, с. 151-181; Регуляторные механизмы клетки, пер. с англ., М., 1964; Петрушенко Л.А., Принцип обратной связи, М., 1967: Винер Н., Кибернетика или управление и связь в животном и машине, пер. с англ., М., 1968; Шмальгаузен И. И., Кибернетические вопросы биологии, Новосибирск, 1968. А. А. Малиновский. 
Рис. 1. Схемы усилителей с различными видами цепей обратной связи: а - последовательная обратная связь по току; б - последовательная обратная связь по напряжению; в - параллельная обратная связь по току; г - параллельная обратная связь по напряжению. 1 - усилитель электрических колебаний; 2 - цепь обратной связи (стрелкой показано направление распространения сигнала по цепи обратной связи от её входных зажимов к выходным): Z ист- полное сопротивление источника сигнала Е ист; Z нагр- полное нагрузочное сопротивление усилителя. 
Рис. 2. Ламповый усилитель электрических колебаний с обратной связью: U вх- напряжение на входе усилителя; Л - электронная лампа; R- резистор в цепи катода лампы; Lи С- соответственно индуктивность и ёмкость колебательного контура в цепи анода лампы; М- взаимная индуктивность, связывающая цепи анода и управляющей сетки лампы; U вых- напряжение на выходе усилителя; E a- напряжение анодного питания. Обратная сила закона Обра'тная си'ла зако'на, распространение действия закона на отношения, возникшие до его издания. Как правило, закон обратной силы не имеет, т. е. он применяется только к отношениям, правам и обязанностям, которые возникли после вступления данного закона в силу. Это вносит определённость и устойчивость в общественную жизнь, в осуществление правовых предписаний, создаёт у граждан уверенность в незыблемости их прав и обязанностей, предусмотренных действующими законами. При необходимости законодатель может специальным указанием придать тому или иному закону (иногда некоторым статьям закона) обратную силу, т. е. распространить вновь принятый закон на отношения, которые возникли ранее. В СССР обратная сила придаётся также уголовным законам, устраняющим наказуемость деяния или смягчающим меру наказания. В этом проявляется гуманизм советского права, исходящего из нецелесообразности наказывать вообще (или наказывать столь же строго) за действие, которое ранее считалось преступлением, а к моменту выхода нового закона потеряло прежний социально опасный характер. Наряду с принципом О. с. з. (т. н. ретроактивность) возможно также «переживание старого закона», т. е. распространение действия закона, потерявшего силу, на отношения, имеющие место после его отмены (т. н. ультраактивность). Обратная теорема Обра'тная теоре'ма, теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением - условие. Обратной к О. т. будет исходная (прямая) теорема. Таким образом, прямая и О. т. взаимно обратны. Например, теоремы: «если два угла треугольника равны, то их биссектрисы равны» и «если две биссектрисы треугольника равны, то соответствующие им углы равны» - являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: «если число делится на 6, то оно делится на 3» - верна, а О. т.: «если число делится на 3, то оно делится на 6» - неверна. Даже если О. т. верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема «две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются», так и обратная к ней теорема «две непересекающиеся прямые на плоскости имеют общий перпендикуляр». Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. О. т. равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный способ «доказательства от противного» как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения (см. Необходимые и достаточные условия ). Обратная функция
Обра'тная фу'нкция,
функция
, обращающая зависимость, выражаемую данной функцией. Так, если
у = f(
x) - данная функция, то переменная
х, рассматриваемая как функция переменной
у,
х =j (
y), является обратной по отношению к данной функции
у = f (x). Например, О. ф. для
у = ax + b (а¹0)является
х = (у-b)/a, О. ф. для
у = е
хявляется
х= ln
уи т.д. Если
х =j(
y) есть О. ф. по отношению к
у=
f (x),то и
у=
f (x)есть О. ф. по отношению к
х =j(
y). Областью определения О. ф. является область значений данной функции, а областью значений О. ф.- область определения данной. Графики двух взаимно обратных функций
у = f (x) и у =j
(x)(где независимое переменное обозначено одной и той же буквой
х), как, например,
у = ax+
bи
у = (х-b)/a, у = е
хи
у = ln
х, симметричны по отношению к биссектрисе
у = хпервого и третьего координатных углов. Функция, обратная по отношению к однозначной функии, может быть многозначной (ср., например, функции
х
2и
Если данная функция кусочно монотонна, то, разбивая область её определения на участки её монотонности, получают однозначные ветви О. ф. Так, одним из участков монотонности для sin хслужит интервал - p/2< x< p/2; ему соответствует т. н. главная ветвь arc sin хобратной функции Arc sin х. Для пары однозначных взаимно обратных функций имеют место соотношения j [f (x)]=xи f [j (x)] = х, первое из которых справедливо для всех значений хиз области определения функции f (x),а второе - для всех значений хиз области определения функции j (x); например, e ln x = х(х > 0), 1n (e x ) = х(- Ґ < х < Ґ). Иногда функцию, обратную к f (x) =у, обозначают f - -1(y)= х, так что для непрерывной и монотонной функции f (x): F -1[f (x)]=f [f -1)x)]=x. Вообще же f --1[f (x)]представляет собой многозначную функцию от х, одним из значений которой является х; так, для f (x)= x 2, х(¹ 0) является лишь одним из двух значений f --1[f (x)] = x 2(другое: -х); для f (x)= sin х, хявляется лишь одним из бесконечного множества значений f - -1[f (x)]= Arc sin [sin x] = (-1) n x + np, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31 |
|||||||
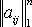 порядка n такая матрица
В=
порядка n такая матрица
В=
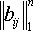 (того же порядка), что
АВ = Е, где
Е- единичная матрица; тогда выполняется также и равенство
ВА = Е. О. м. обозначается через
А
-1. Для существования О. м.
А
-1необходимо и достаточно, чтобы
определитель
данной матрицы
Абыл отличен от нуля, т. е. чтобы матрица
Абыла неособенной; элементы
b
ijО. м. находятся по формуле
b
ij=
A
jii/D, где
A
jii- алгебраическое дополнение элемента
a
ijматрицы
A, a
D- определитель матрицы
А.
(того же порядка), что
АВ = Е, где
Е- единичная матрица; тогда выполняется также и равенство
ВА = Е. О. м. обозначается через
А
-1. Для существования О. м.
А
-1необходимо и достаточно, чтобы
определитель
данной матрицы
Абыл отличен от нуля, т. е. чтобы матрица
Абыла неособенной; элементы
b
ijО. м. находятся по формуле
b
ij=
A
jii/D, где
A
jii- алгебраическое дополнение элемента
a
ijматрицы
A, a
D- определитель матрицы
А.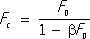
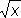 ). Для однозначности О. ф. необходимо и достаточно, чтобы данная функция
у=
f (x)принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О. ф. по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.
). Для однозначности О. ф. необходимо и достаточно, чтобы данная функция
у=
f (x)принимала различные значения для различных значений аргумента. Для непрерывной функции последнее условие может выполняться только в том случае, если данная функция монотонна (имеются в виду функции действительного аргумента, принимающие действительные значения). О. ф. по отношению к непрерывной и монотонной функции однозначна, непрерывна и монотонна.