 |
|
Популярные авторы:: БСЭ :: Лондон Джек :: Чехов Антон Павлович :: Завтра Газета :: Горький Максим :: Андерсон Пол Уильям :: Лесков Николай Семёнович :: Раззаков Федор :: Громов Дмитрий :: Говард Роберт Ирвин Популярные книги:: Бурый волк :: Справочник по реестру Windows XP :: Лётчики :: ЛСД – мой трудный ребёнок :: Похититель снов :: Человек имеет право :: К новому солнцу :: Идет розыск [Полный вариант] :: Учимся читать быстро :: Учебное пособие по социальной философии |
Большая Советская Энциклопедия (ТО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТО) - Чтение (стр. 23)
Эта простая и наглядная операция оказывается очень важной, так как позволяет получать из сравнительно простых топологических пространств более сложные. Если
Yсостоит из одной точки, то пространство
ХИ
fYобозначается символом
Х/Аи о нём говорят, что оно получено из
Хстягиванием
Ав точку. Например, если
Х- диск, а
А- его граничная окружность, то
Х/Агомеоморфно сфере.
2. Равномерная топология Часть Т., изучающая аксиоматическое понятие равномерной непрерывности, называется равномерной Т. Известное из анализа определение равномерной непрерывности числовых функций непосредственно переносится на отображения любых метрических пространств. Поэтому аксиоматику равномерной непрерывности обычно получают, отталкиваясь от метрических пространств. Подробно исследованы два аксиоматических подхода к равномерной непрерывности, основанных соответственно на понятиях близости и окружения диагонали. Подмножества
Аи
Вметрических пространства
Хназываются близкими (обозначение
Ad
B)
,если для любого e > 0 существуют точки
aО
Аи
bО
В,расстояние между которыми < e. Принимая основные свойства этого отношения за аксиомы, приходят к следующему определению: (отделимой) структурой близости на множестве
Хназывается такое отношение d на множестве всех его подмножеств, что: 1) Ж
Другой подход основан на том, что равномерную непрерывность в метрическом пространстве Хможно определить в терминах отношения «точки хи унаходятся на расстоянии, не большем e». С общей точки зрения, отношение на Хесть не что иное как произвольное подмножество Uпрямого произведения Хґ X. Отношение «тождество» является с этой точки зрения диагональю D М Хґ X, то есть множеством точек вида ( х, х), хО X.Для любого отношения Uопределено обратное отношение U -1= {( х, у); ( у, х) О U} и для любых двух отношений Uи Vопределена их композиция UЧ V= {( х, у); существует zО Хтакое, что ( х, z) О U, ( z, y) О V}. Семейство отношений { U} называется (отделимой) равномерной структурой на Х(а отношения Uназывается окружениями диагонали), если: 1) пересечение любых двух окружений диагонали содержит окружение диагонали; 2) каждое окружение диагонали содержит D, и пересечение всех окружений диагонали совпадает с D; 3) вместе с Uокружением диагонали является и U -1; 4) для любого окружения диагонали Uсуществует такое окружение диагонали W, что Wo WМ U. Множество, наделённое равномерной структурой, называется равномерным пространством. Отображение f: X® Yравномерного пространства Хв равномерное пространство Yназывается равномерно непрерывным, если прообраз при отображении fґ f: Хґ Х® Yґ Yлюбого окружения диагонали VМ Yґ Yсодержит некоторое окружение диагонали из Хґ X. Равномерные пространства Хи Yназываются равномерно гомеоморфными, если существует взаимно однозначное равномерно непрерывное отображение Х® Y, обратное к которому также является равномерно непрерывным отображением. В равномерной Т. такие равномерные пространства считаются одинаковыми. Каждая равномерная структура на Хопределяет некоторую структуру близости: Аd Втогда и только тогда, когда ( Aґ В) З U¹ Ж для любого окружения диагонали UМ Xґ X. При этом равномерно непрерывные отображения оказываются близостно непрерывными. 3. Алгебраическая топология
Пусть каждому топологическому пространству
Х(из некоторого класса) поставлен в соответствие некоторый алгебраический объект
h(X)(группа, кольцо и т.п.), а каждому непрерывному отображению
f:
X®
Y -некоторый гомоморфизм
h(f):
h(X)®
h(Y)(или
h(f):
h(Y)®
h(X),являющийся тождественным гомоморфизмом, когда
fпредставляет собой тождественное отображение. Если
h(f
1
Вообще говоря, установление несуществования гомоморфизма (j тем легче, чем сложнее алгебраическая структура объектов h(X).Поэтому в алгебраических Т. рассматриваются алгебраические объекты чрезвычайно сложной природы, и требования алгебраической топологии существенно стимулировали развитие абстрактной алгебры. Топологическое пространство Хназывается клеточным пространством, а также клеточным разбиением (или CW-комплексом), если в нём указана возрастающая последовательность подпространств X 0М ¼ М X n-1М X nМ ¼ (называется остовами клеточного пространства X), объединением которых является всё X, причём выполнены следующие условия: 1) множество UМ Xтогда и только тогда открыто в X, когда для любого nмножество UЗ X nоткрыто в X n; 2) X nполучается из X n-1приклеиванием некоторого семейства n-мepных шаров по их граничным ( n-1)-мepным сферам (посредством произвольного непрерывного отображения этих сфер в X n-1); 3) X 0состоит из изолированных точек. Таким образом, структура клеточного пространства состоит, грубо говоря, в том, что оно представлено в виде объединения множеств, гомеоморфных открытым шарам (эти множества называются клетками). В алгебраических Т. изучаются почти исключительно клеточные пространства, поскольку специфика задач алгебраических Т. для них уже полностью проявляется. Более того, фактически для алгебраических Т. интересны некоторые особо простые клеточные пространства (типа полиэдров , см. ниже), но сужение класса клеточных пространств, как правило, существенно осложняет исследование (поскольку многие полезные операции над клеточными пространствами выводят из класса полиэдров). Два непрерывных отображения f, g: X® Yназываются гомотопными, если они могут быть непрерывно продеформированы друг в друга, то есть если существует такое семейство непрерывных отображений f t: X® Y,непрерывно зависящих от параметра tО [0, 1], что f 0= fи f 1= g(непрерывная зависимость от tозначает, что формула F(x, t) = f t(x), хО X, tО [0, 1] определяет непрерывное отображение F: Хґ [0, 1] ® Y; это отображение, а также семейство {f t}называют гомотопией, связывающей fс g). Совокупность всех непрерывных отображений X® Yраспадается на гомотопические классы гомотопных между собой отображений. Множество гомотопических классов непрерывных отображений из Хв Yобозначается символом [ X, Y]. Изучение свойств отношения гомотопности и, в частности, множеств [ X, Y] составляет предмет так называемой гомотопической топологии (или теории гомотопий). Для большинства интересных топологических пространств множества [ X, Y] конечны или счётны и могут быть в явном виде эффективно вычислены. Топологические пространства Хи Yназываются гомотопически эквивалентными, или имеющими один и тот же гомотопический тип, если существуют такие непрерывные отображения f: Х® Yи g: Y® Х, что непрерывные отображения gЧf: Х® Хи fЧg: Y® Yгомотопны соответствующим тождественным отображениям. В гомотопической Т. такие пространства следует рассматривать как одинаковые (все их «гомотопические инварианты» совпадают). Оказывается, что во многих случаях (в частности, для клеточных пространств) разрешимость задачи распространения зависит только от гомотопического класса непрерывного отображения f: A® Y; точнее, если для fраспространение g: Х® Yсуществует, то для любой гомотопии f t: A® Y (с f 0= f)существует распространение g t: Х® Yтакое, что g 0= g. Поэтому вместо fможно рассматривать его гомотопический класс [f]и в соответствии с этим изучать лишь гомотопически инвариантные функторы (кофункторы) h, то есть такие, что h(f 0)= h(f 1),если отображения f 0и f 1гомотопны. Это приводит к настолько тесному переплетению алгебраической и гомотопической Т., что их можно рассматривать как единую дисциплину. Для любого топологического пространства
Yформулы
h(X)= [
X,
Y] и
h(f)
= [j
Аналогичным («двойственным») образом, каждое топологическое пространство
Yзадаёт по формулам
h(X)
=[
Y,
X],
h(f)=
[
f
Клеточное пространство Хназывается пространством K( G, n), если p i (X) =0 при i¹ nи p n X= G; такое клеточное пространство существует для любого n³ 1 и любой группы G(коммутативной при n> 1) и с точностью до гомотопической эквивалентности определено однозначно. При n> 1 (а также при n= 1, если группа Gкоммутативна) пространство K( G, n) оказывается Н-пространством и потому представляет некоторую группу H n (X; G)= [ X; K(G, n)]. Эта группа называется n-мepной группой когомологий топологического пространства Хс группой коэффициентов G. Она является типичным представителем целого ряда важных кофункторов, к числу которых принадлежит, например, К-функтор KO(X)= [ Х, BO], представляемый так называемым бесконечномерным грассманианом BO, группы ориентированных кобордизмов W n Xи т.п. Если
Gявляется кольцом, то прямая сумма
Н*(Х; G)групп
H
n(X; G)является алгеброй над
G. Более того, эта прямая сумма обладает очень сложной алгебраической структурой, в которую (при
G=
Z
p, где
Z
p- циклическая группа порядка
р) входит действие на
Н*(Х; G)некоторой некоммутативной алгебры
Исторически группам когомологий предшествовали так называемые группы гомологий H n(X; G), являющиеся гомотопическими группами p n M(X, G)некоторого клеточного пространства M(X, G), однозначно строящегося по клеточному пространству Хи группе G. Группы гомологий и когомологий в определённом смысле двойственны друг другу, и их теории по существу равносильны. Однако алгебраическая структура, имеющаяся в группах гомологий, менее привычна (например, эти группы составляют не алгебру, а так называемую коалгебру), и поэтому в вычислениях обычно пользуются группами когомологий. Вместе с тем в некоторых вопросах группы гомологий оказываются более удобными, поэтому они также изучаются. Часть алгебраических Т., занимающаяся изучением (и применением) групп гомологий и когомологий, называется теорией гомологий. Перенесение результатов алгебраических Т. на пространства более общие, чем клеточные пространства, составляет предмет так называемой общей алгебраической Т. В частности, общая теория гомологий изучает группы гомологий и когомологий произвольных топологических пространств и их применения. Оказывается, что вне класса компактных клеточных пространств различные подходы к построению этих групп приводят, вообще говоря, к различным результатам, так что для неклеточных топологических пространств возникает целый ряд различных групп гомологий и когомологий. Основное применение общая теория гомологий находит в теории размерности и в теории так называемых законов двойственности (описывающих взаимоотношения между топологическими свойствами двух дополнительных подмножеств топологического пространства), и её развитие было во многом стимулировано нуждами этих теорий. 4. Кусочно-линейная топология
Подмножество Р О
Подмножество
ХО
а) симплекс, вершины которого определённым образом упорядочены, называется упорядоченным симплексом данной триангуляции (или симплициальной схемы) К; формальные линейные комбинации упорядоченных симплексов данной размерности nс коэффициентами из данной группы Gназываются n-мepными цепями; все они естественным образом составляют группу, которая обозначается символом C n (K; G); б) выбросив из упорядоченного
n-мерного симплекса s вершину с номером
i, 0 Ј
iЈ
n,получим упорядоченный (
n-1)-мерный симплекс, который обозначается символом s
(
i); цепь
в) цепи
с, для которых
г) цепи вида
д) доказывается, что B n(K; G)М Z n(K; G)(граница является циклом); поэтому определена факторгруппа H n(K; G) = Z n(K; G)/ B n(K; G). Оказывается, что группа H n(K; G)изоморфна группе гомологий H n(X; G)полиэдра X, триангуляцией которого является К. Аналогичная конструкция, в которой исходят не из цепей, а из коцепей (произвольных функций, определённых на множестве всех упорядоченных симплексов и принимающих значения в G), даёт группы когомологий. С этой конструкции, изложенной здесь в несколько модифицированной форме, и началось по существу становление алгебраической Т. В первоначальной конструкции рассматривались так называемые ориентированные симплексы (классы упорядоченных симплексов, отличающихся чётными перестановками вершин). Эта конструкция развита и обобщена в самых разнообразных направлениях. В частности, её алгебраические аспекты дали начало так называемой гомологической алгебре. Самым общим образом симплициальную схему можно определить как множество, в котором отмечены некоторые конечные подмножества («симплексы»), причём требуется, чтобы любое подмножество симплекса было снова симплексом. Такая симплициальная схема является симплициальной схемой триангуляции некоторого полиэдра тогда и только тогда, когда число элементов произвольного отмеченного подмножества не превосходит некоторого фиксированного числа. Впрочем, понятие полиэдра можно обобщить (получив так называемые «бесконечномерные полиэдры»), и тогда уже любая симплициальная схема будет схемой триангуляции некоторого полиэдра (называемого её геометрической реализацией). Произвольному открытому покрытию { U a} каждого топологического пространства Хможно сопоставить симплициальную схему, вершинами которой являются элементы U aпокрытия и подмножество которой тогда и только тогда отмечено, когда элементы покрытия, составляющие это подмножество, имеют непустое пересечение. Эта симплициальная схема (и соответствующий полиэдр) называемому нервом покрытия. Нервы всевозможных покрытий в определённом смысле аппроксимируют пространство Хи, исходя из их групп гомологий и когомологий, можно посредством соответствующего предельного перехода получать группы гомологий и когомологий самого X. Эта идея лежит в основе почти всех конструкций общей теории гомологий. Аппроксимация топологического пространства нервами его открытых покрытий играет важную роль и в общей Т. 5. Топология многообразий
Хаусдорфово паракомпактное топологическое пространство называется
n-мерным топологическим многообразием, если оно «локально евклидово», то есть если каждая его точка обладает окрестностью (называемой координатной окрестностью, или картой), гомеоморфной топологическому пространству
Условимся произвольный гомеоморфизм между открытыми множествами из
Пусть a = t, pили s.Топологическое многообразие называется a-многообразием, если выбрано такое его покрытие картами, что гомеоморфизмы перехода для любых его двух (пересекающихся) карт являются a-гомеоморфизмами. Такое покрытие задаёт a-структуру на топологическом многообразии X. Таким образом, t-многообразие - это просто любое топологическое многообразие, p-многообразия называются кусочно-линейными многообразиями. Каждое кусочно-линейное многообразие является полиэдром. В классе всех полиэдров n-мерные кусочно-линейные многообразия характеризуются тем, что любая их точка обладает окрестностью, кусочно-линейно изоморфной n-мерному кубу. s-многообразия называются гладкими (или дифференцируемыми) многообразиями. a-отображением a-многообразия называются называется при a = tпроизвольное непрерывное отображение, при a = s -произвольное кусочно-линейное отображение, при a = s -произвольное гладкое отображение, то есть непрерывное отображение, записывающееся в локальных координатах гладкими функциями. Взаимно однозначное a-отображение, обратное к которому также является a-отображением, называется a-гомеоморфизмом (при a = sтакже диффеоморфизмом), a-многообразия Хи Yназываются a-гомеоморфными (при a = s -диффеоморфными), если существует хотя бы один a-гомеоморфизм X® Y. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36 |
|||||||
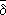 X(символом
X(символом
 обозначается отрицание отношения d; 2)
A
обозначается отрицание отношения d; 2)
A
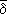 B
1и
A
B
1и
A
 B
2Ы
A
B
2Ы
A
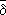 (
B
1U
B
2)
; 3)
{
x}
(
B
1U
B
2)
; 3)
{
x}
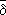 {
y} Ы
x¹
y; 4) если
А
{
y} Ы
x¹
y; 4) если
А
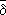 В, то существует такое множество
С
В, то существует такое множество
С
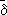 В, что
А
В, что
А
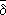 (
Х \
С)
.Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости
Хв пространство близости
Yназывается близостно непрерывным, если образы близких в
Хмножеств близки в
Y. Пространства близости
Хи
Yназываются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение
X®
Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Т. эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество
uМ
xоткрытым, если {
x}
(
Х \
С)
.Множество, в котором задана структура близости, называется пространством близости. Отображение пространства близости
Хв пространство близости
Yназывается близостно непрерывным, если образы близких в
Хмножеств близки в
Y. Пространства близости
Хи
Yназываются близостно гомеоморфными (или эквиморфными), если существует взаимно однозначное близостно непрерывное отображение
X®
Y, обратное к которому также является близостно непрерывным (такое близостно непрерывное отображение называется эквиморфизмом). В равномерной Т. эквиморфные пространства близости рассматриваются как одинаковые. Подобно метрическим пространствам, любое пространство близости можно превратить в (хаусдорфово) топологическое пространство, считая подмножество
uМ
xоткрытым, если {
x}
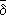 (
X\
U) для любой точки
хО
U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства
Хвсе структуры близости на
X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии - би-компактными расширениями)
вХ- компактными хаусдорфовыми топологическими пространствами, содержащими
Хв качестве всюду плотного пространства. Структура близости d, соответствующая расширению
вХ,характеризуется тем, что
Аd
Втогда и только тогда, когда замыкания множеств
Аи
Впересекаются в
bX. В частности, на любом компактном хаусдорфовом топологическом пространстве
Хсуществует единственная структура близости, порождающая его топологическую структуру.
(
X\
U) для любой точки
хО
U. При этом близостно непрерывные отображения окажутся непрерывными отображениями. Класс топологических пространств, получающихся описанным образом из пространств близости, совпадает с классом вполне регулярных топологических пространств. Для любого вполне регулярного пространства
Хвсе структуры близости на
X, порождающие его топологическую структуру, находятся во взаимно однозначном соответствии с так называемыми компактификациями (в другой терминологии - би-компактными расширениями)
вХ- компактными хаусдорфовыми топологическими пространствами, содержащими
Хв качестве всюду плотного пространства. Структура близости d, соответствующая расширению
вХ,характеризуется тем, что
Аd
Втогда и только тогда, когда замыкания множеств
Аи
Впересекаются в
bX. В частности, на любом компактном хаусдорфовом топологическом пространстве
Хсуществует единственная структура близости, порождающая его топологическую структуру. f
2)
= h(f
1)
f
2)
= h(f
1)
 h(f
2)(или, соответственно,
h(f
1
h(f
2)(или, соответственно,
h(f
1
 f
2)
= h(f
2)
f
2)
= h(f
2)
 h(f
1),то говорят, что
hпредставляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Т. так или иначе связано со следующей задачей распространения: для данного непрерывного отображения
f : A®
Yподпространства
AМ Х в некоторое топологическое пространство
Yнайти непрерывное отображение
g : X®
Y, совпадающее на
Aс
f, то есть такое, что
f
=
gЧi, где
i
:
А®
Х
-отображение вложения (
i(a)=
адля любой точки а О
A). Если такое непрерывное отображение
gсуществует, то для любого функтора (кофунктора)
hсуществует такой гомоморфизм (j:
h(X)®
h(Y)(гомоморфизм j:
h(Y)®
h(X)), что
h(f) =j
h(f
1),то говорят, что
hпредставляет собой функтор (соответственно кофунктор). Большинство задач алгебраической Т. так или иначе связано со следующей задачей распространения: для данного непрерывного отображения
f : A®
Yподпространства
AМ Х в некоторое топологическое пространство
Yнайти непрерывное отображение
g : X®
Y, совпадающее на
Aс
f, то есть такое, что
f
=
gЧi, где
i
:
А®
Х
-отображение вложения (
i(a)=
адля любой точки а О
A). Если такое непрерывное отображение
gсуществует, то для любого функтора (кофунктора)
hсуществует такой гомоморфизм (j:
h(X)®
h(Y)(гомоморфизм j:
h(Y)®
h(X)), что
h(f) =j
 h(i)(соответственно
h(f) =
h(i)
h(i)(соответственно
h(f) =
h(i)
 j); им будет гомоморфизм j
= h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора
h) влечёт несуществование отображения
g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Т. Например, существует функтор
h, значение которого на шаре
E
nявляется тривиальной, а на ограничивающей шар сфере
S
n-1- нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции - непрерывного отображения
р:
E
n®
S
n-1, неподвижного на
S
n-1, то есть такого, что композиция
рЧi,где
i:
S
n1
®
E
n
-отображение вложения, представляет собой тождественное отображение (если
рсуществует, то тождественное отображение группы
h(S
n-1)будет композицией отображений
h(i):
h(S
n-1)®
h(E
n)и
h(p):
h(E
n)®
h(S
n-1),что при тривиальной группе
h(E
n)невозможно). Однако этот, по существу, элементарно-геометрический и (при
n
=2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение
f:
E
n®
E
nимеет хотя бы одну неподвижную точку, то есть уравнение
f(x) = химеет в
E
nхотя бы одно решение (если
f(x)¹
xдля всех
хО
E
n, то, приняв за
р(х)точку из
S
n-1, коллинеарную точкам
f(x)и
хи такую, что отрезок с концами
f(x)и
р(х)содержит
х, получим ретракцию
р:
E
n®
S
n-1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Т., а затем явилась источником целой серии разнообразных теорем существования решений уравнений.
j); им будет гомоморфизм j
= h(g). Следовательно, несуществование гомоморфизма j (хотя бы для одного функтора
h) влечёт несуществование отображения
g. К этому простому принципу могут быть фактически сведены почти все методы алгебраических Т. Например, существует функтор
h, значение которого на шаре
E
nявляется тривиальной, а на ограничивающей шар сфере
S
n-1- нетривиальной группой. Уже отсюда следует отсутствие так называемой ретракции - непрерывного отображения
р:
E
n®
S
n-1, неподвижного на
S
n-1, то есть такого, что композиция
рЧi,где
i:
S
n1
®
E
n
-отображение вложения, представляет собой тождественное отображение (если
рсуществует, то тождественное отображение группы
h(S
n-1)будет композицией отображений
h(i):
h(S
n-1)®
h(E
n)и
h(p):
h(E
n)®
h(S
n-1),что при тривиальной группе
h(E
n)невозможно). Однако этот, по существу, элементарно-геометрический и (при
n
=2) наглядно очевидный факт (физически означающий возможность натянуть на круглый обруч барабан) до сих пор не удалось доказать без привлечения алгебраико-топологических методов. Его непосредственным следствием является утверждение, что любое непрерывное отображение
f:
E
n®
E
nимеет хотя бы одну неподвижную точку, то есть уравнение
f(x) = химеет в
E
nхотя бы одно решение (если
f(x)¹
xдля всех
хО
E
n, то, приняв за
р(х)точку из
S
n-1, коллинеарную точкам
f(x)и
хи такую, что отрезок с концами
f(x)и
р(х)содержит
х, получим ретракцию
р:
E
n®
S
n-1). Эта теорема о неподвижной точке была одной из первых теорем алгебраической Т., а затем явилась источником целой серии разнообразных теорем существования решений уравнений. f],где f :
X
1®
X
2и j :
X
2®
Y,определяют некоторый гомотопически инвариантный кофунктор
h, о котором говорят, что он представлен топологическим пространством
Y. Это - стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество
h(
X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в
Хнекоторую точку
x
0и рассматривать лишь непрерывные отображения и гомотопии, переводящие
x
0в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы
Yбыло топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются
Н-пространствами. Таким образом, каждое
Н-пространство
Yзадаёт гомотопически инвариантный кофунктор
h(X)= [
X,
Y], значениями которого являются группы.
f],где f :
X
1®
X
2и j :
X
2®
Y,определяют некоторый гомотопически инвариантный кофунктор
h, о котором говорят, что он представлен топологическим пространством
Y. Это - стандартный (и по существу единственный) приём построения гомотопических инвариантных кофункторов. Чтобы множество
h(
X) оказалось, скажем, группой, нужно У выбрать соответствующим образом, например потребовать, чтобы оно было топологической группой (вообще говоря, это не совсем так: необходимо выбрать в
Хнекоторую точку
x
0и рассматривать лишь непрерывные отображения и гомотопии, переводящие
x
0в единицу группы; это техническое усложнение будет, однако, в дальнейшем игнорироваться). Более того, достаточно, чтобы
Yбыло топологической группой «в гомотопическом смысле», то есть чтобы аксиомы ассоциативности и существования обратного элемента (утверждающие фактически совпадение некоторых отображений) выполнялись бы только «с точностью до гомотопии». Такие топологические пространства называются
Н-пространствами. Таким образом, каждое
Н-пространство
Yзадаёт гомотопически инвариантный кофунктор
h(X)= [
X,
Y], значениями которого являются группы. j], где
f:
X
1®
X
2и j :
Y®
X
1, некоторый функтор
h. Чтобы
h(X)было группой, нужно, чтобы
Yобладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре
Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-
Н-пространствами. Примером ко-
Н-пространства является
n-мepная сфера
S
n(при
n³
1). Таким образом, для любого топологического пространства
Хформула p
n
X
=[
S
n,
X] определяет некоторую группу p
n
X,
n³
1, которая называется
n-й гомотопической группой пространства
X. При
n= 1 она совпадает с фундаментальной группой. При
n> 1 группа p
n
Xкоммутативна. Если p
1
X = {1}, то
Хназывается односвязным.
j], где
f:
X
1®
X
2и j :
Y®
X
1, некоторый функтор
h. Чтобы
h(X)было группой, нужно, чтобы
Yобладало определённой алгебраической структурой, в некотором точно определённом смысле двойственной структуре
Н-пространства. Топологические пространства, наделённые этой структурой, называются ко-
Н-пространствами. Примером ко-
Н-пространства является
n-мepная сфера
S
n(при
n³
1). Таким образом, для любого топологического пространства
Хформула p
n
X
=[
S
n,
X] определяет некоторую группу p
n
X,
n³
1, которая называется
n-й гомотопической группой пространства
X. При
n= 1 она совпадает с фундаментальной группой. При
n> 1 группа p
n
Xкоммутативна. Если p
1
X = {1}, то
Хназывается односвязным.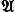 p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп
H
n(X; G),а с другой - установить связи между группами
H
n(X; G)и другими гомотопически инвариантными функторами (например, гомотопическими группами p
n
X), позволяющие часто в явном виде вычислить и эти функторы.
p, называемой алгеброй Стинрода. Сложность этой структуры позволяет, с одной стороны, выработать эффективные (но совсем не простые) методы вычисления групп
H
n(X; G),а с другой - установить связи между группами
H
n(X; G)и другими гомотопически инвариантными функторами (например, гомотопическими группами p
n
X), позволяющие часто в явном виде вычислить и эти функторы.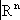 называется конусом с вершиной
аи основанием
В, если каждая его точка принадлежит единственному отрезку вида
ab, где
bО
В.Подмножество
ХО
называется конусом с вершиной
аи основанием
В, если каждая его точка принадлежит единственному отрезку вида
ab, где
bО
В.Подмножество
ХО
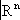 называется полиэдром, если любая его точка обладает в
Хокрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение
f:
X®
Yполиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки
хО
X.Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Т. является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Т. полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.
называется полиэдром, если любая его точка обладает в
Хокрестностью, замыкание которой является конусом с компактным основанием. Непрерывное отображение
f:
X®
Yполиэдров называется кусочно-линейным, если оно линейно на лучах каждой конической окрестности любой точки
хО
X.Взаимно однозначное кусочно-линейное отображение, обратное к которому также кусочно-линейно, называется кусочно-линейным изоморфизмом. Предметом кусочно-линейной Т. является изучение полиэдров и их кусочно-линейных отображений. В кусочно-линейной Т. полиэдры считаются одинаковыми, если они кусочно-линейно изоморфны.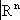 тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения
симплексов
, пересекающихся только по целым граням. Такое представление называют
триангуляцией
полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом:
тогда и только тогда является (компактным) полиэдром, когда оно представляет собой объединение (конечного) семейства выпуклых многогранников. Любой полиэдр может быть представлен в виде объединения
симплексов
, пересекающихся только по целым граням. Такое представление называют
триангуляцией
полиэдра. Каждая триангуляция однозначно определена её симплициальной схемой, то есть множеством всех её вершин, в котором отмечены подмножества, являющиеся множествами вершин симплексов. Поэтому вместо полиэдров можно рассматривать лишь симп-лициальные схемы их триангуляций. Например, по симплициальной схеме можно вычислять группы гомологий и когомологий. Это делается следующим образом: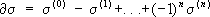 называется границей s;
по линейности отображение
называется границей s;
по линейности отображение
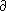 распространяется до гомоморфизма
распространяется до гомоморфизма
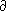 :
C
n(K; G)®
C
n
-1
(K; G);
:
C
n(K; G)®
C
n
-1
(K; G);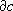 = 0, называются циклами, они составляют группу циклов
Z
n(K; G);
= 0, называются циклами, они составляют группу циклов
Z
n(K; G);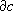 называются границами, они составляют группу границ
B
n(K; G);
называются границами, они составляют группу границ
B
n(K; G);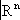 . В этой окрестности точки задаются
nчислами
x
1,…
, x
n,называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в
. В этой окрестности точки задаются
nчислами
x
1,…
, x
n,называемыми локальными координатами. В пересечении двух карт соответствующие локальные координаты выражаются друг через друга посредством некоторых функций, называемых функциями перехода. Эти функции задают гомеоморфизм открытых множеств в
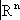 , называются гомеоморфизмом перехода.
, называются гомеоморфизмом перехода.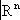 называть
t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть
p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, -
s-гомеоморфизмом.
называть
t-гомеоморфизмом. Гомеоморфизм, являющийся кусочно-линейным изоморфизмом, будем называть
p-гомеоморфизмом, а если он выражается гладкими (дифференцируемыми любое число раз) функциями, -
s-гомеоморфизмом.