 |
|
Популярные авторы:: Лондон Джек :: БСЭ :: Чехов Антон Павлович :: Завтра Газета :: Лесков Николай Семёнович :: Горький Максим :: Андерсон Пол Уильям :: Громов Дмитрий :: Твен Марк :: Нортон Андрэ Популярные книги:: Бурый волк :: Справочник по реестру Windows XP :: Лётчики :: ЛСД – мой трудный ребёнок :: Похититель снов :: Человек имеет право :: К новому солнцу :: Учимся читать быстро :: Учебное пособие по социальной философии :: Паутина Лайгаша [=Ворон] |
Большая Советская Энциклопедия (ТО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТО) - Чтение (стр. 24)
Предметом теории a-многообразий является изучение a-многообразий и их a-отображений; при этом a-гомеоморфные a-многообразия считаются одинаковыми. Теория
s-многообразий является частью кусочно-линейной Т. Теория
s-многообразий называется также гладкой Т.
Основной метод современной теории многообразий состоит в сведении её задач к проблемам алгебраических Т. для некоторых нужным образом сконструированных топологических пространств. Эта тесная связь теории многообразий с алгебраической Т. позволила, с одной стороны, решить много трудных геометрических проблем, а с другой - резко стимулировала развитие самой алгебраической Т. Примерами гладких многообразий являются
n-мерные поверхности в
Каждое p-многообразие является t-многообразием. Оказывается, что на любом s-многообразии можно некоторым естественным образом ввести p-структуру (которая называется обычно у айтхедовской триангуляцией). Можно сказать, что любое a-многообразие, где a = pили s,является a’-многообразием, где a’ = tили p. Ответ на обратный вопрос: на каких a’-многообразиях можно ввести a-структуру (такое a’-многообразие при a’ = pназывается сглаживаемым, а при a’ = t - триангулируемым), а если можно, то сколько? - зависит от размерности n.
Существует только два одномерных топологических многообразия: окружность
S
1(компактное многообразие) и прямая линия
Аналогично, на любом двумерном топологическом многообразии (поверхности) существует единственная a-структура, и можно легко описать все компактные связные поверхности (некомпактные связные поверхности также могут быть описаны, но ответ получается более сложный). Для того чтобы поверхности были гомеоморфны, достаточно, чтобы они были гомотопически эквивалентны. При этом гомотопический тип любой поверхности однозначно характеризуется её группами гомологий. Существует два типа поверхностей: ориентируемые и неориентируемые. К числу ориентируемых принадлежит сфера
S
2и тор
T
2.Пусть
Хи
Y- два связных
n-мерных a-многообразия. Вырежем в
Хи
Yпо шару (при
n =2 - диску) и склеим получившиеся граничные сферы (при
n= 2 - окружности). При соблюдении некоторых само собой разумеющихся предосторожностей в результате снова получим a-многообразие. Оно называется связной суммой a-многообразий
Хи
Yи обозначается
X#
Y. Например,
T
2#
T
2имеет вид кренделя. Сфера
S
nявляется нулём этого сложения, то есть
S
n#
X=
Хдля любого
X. В частности,
S
2#
T
2
=
T
2. Оказывается, что ориентируемая поверхность гомеоморфна связной сумме вида
S
2#
T
2#
…#
T
2, число
pслагаемых
T
2называется родом поверхности. Для сферы
p= 0, для тора
p= 1 и т. д. Поверхность рода
pможно наглядно представлять себе как сферу, к которой приклеено
p«ручек». Каждая неориентируемая поверхность гомеоморфна связной сумме
На каждом трёхмерном топологическом многообразии при любом a = p, sтакже существует единственная a-структура и можно описать все гомотопические типы трёхмерных топологических многообразий (однако групп гомологий для этого уже недостаточно). В то же время до сих пор (1976) не описаны все (хотя бы компактные связные) трёхмерные топологические многообразия данного гомотопического типа. Это не сделано даже для односвязных многообразий (все они гомотопически эквивалентны сфере S 3). Гипотеза Пуанкаре утверждает, что любое такое многообразие гомеоморфно S 3. Для четырёхмерных (компактных и связных) топологических многообразий вопрос о существовании и единственности a-структур (a = p, s) ещё не решен, а их гомотопический тип описан только в предположении односвязности. Справедлив ли для них аналог гипотезы Пуанкаре, неизвестно. Замечательно, что для компактных и связных топологических многообразий размерности
n³ 5 ситуация оказывается совсем иной: все основные задачи для них можно считать в принципе решенными (точнее, сведёнными к проблемам алгебраической Т.). Любое гладкое многообразие
Хвкладывается как гладкая (
n-мepная) поверхность в
В частности, на сфере S nсуществует единственная кусочно-линейная структура. Гладких структур на сфере S nможет быть много, например, на S 7существует 28 различных гладких структур. На торе T n(топологических произведении nэкземпляров окружности S 1) существует при n³ 5 много различных кусочно-линейных структур, которые все допускают гладкую структуру. Таким образом, начиная с размерности 5, существуют гомеоморфные, но не диффеоморфные гладкие многообразия; сферы с таким свойством существуют, начиная с размерности 7. Задачу описания (с точностью до a-гомеоморфизма) всех n-мерpных ( n³ 5) связных компактных a-многообразий естественно решать в два этапа: искать условия гомотопической эквивалентности a-многообразий и условия a-гомеоморфности гомотопически эквивалентных a-многообразий. Первая задача относится к гомотопической Т. и в её рамках может считаться полностью решенной. Вторая задача также по существу полностью решена (во всяком случае для односвязных a-многообразий). Основой её решения является перенос в высшие размерности техники «разложения на ручки». С помощью этой техники удаётся, например, доказать для n-мерных ( n³ 5) топологических многообразий гипотезу Пуанкаре (связное компактное топологическое многообразие, гомотопически эквивалентное сфере, гомеоморфно ей). Наряду с a-многообразиями можно рассматривать так называемые a-многообразия с краем; они характеризуются тем, что окрестности некоторых их точек (составляющих край) a-гомеоморфны полупространству
X
n³ 0 пространства
Совокупность
М. М. Постников. 6. Основные этапы развития топологии Отдельные результаты топологического характера были получены ещё в 18-19 вв. (теорема Эйлера о выпуклых многогранниках, классификация поверхностей и теорема Жордана о том, что лежащая в плоскости простая замкнутая линия разбивает плоскость на две части). В начале 20 в. создаётся общее понятие пространства в Т. (метрическое - М. Фреше , топологическое - Ф. Хаусдорф ), возникают первоначальные идеи теории размерности и доказываются простейшие теоремы о непрерывных отображениях (А. Лебег , Л. Брауэр ), вводятся полиэдры (А. Пуанкаре ) и определяются их так называемые числа Бетти. Первая четверть 20 в. завершается расцветом общей Т. и созданием московской топологической школы; закладываются основы общей теории размерности (П. С. Урысон ); аксиоматике топологических пространств придаётся её современный вид (П. С. Александров ); строится теория компактных пространств (Александров, Урысон) и доказывается теорема об их произведении (А. Н. Тихонов ); впервые даются необходимые и достаточные условия метризуемости пространства (Александров, Урысон); вводится (Александров) понятие локально конечного покрытия [на основе которого в 1944 Ж. Дьёдонне (Франция) определил паракомпактные пространства]; вводятся вполне регулярные пространства (Тихонов); определяется понятие нерва и тем самым основывается общая теория гомологий (Александров). Под влиянием Э. Нётер числа Бетти осознаются как ранги групп гомологий, которые поэтому называются также группами Бетти. Л. С. Понтрягин , основываясь на своей теории характеров, доказывает законы двойственности для замкнутых множеств. Во 2-й четверти 20 в. продолжается развитие общей Т. и теории гомологий: в развитие идей Тихонова А. Стоун (США) и Э. Чех вводят так называемое стоун - чеховское, или максимальное, (би)компактное расширение вполне регулярного пространства; определяются группы гомологий произвольных пространств (Чех), в группы когомологий (Дж. Александер , А. Н. Колмогоров ) вводится умножение и строится кольцо когомологий. В это время в алгебраической Т. царят комбинаторные методы, основывающиеся на рассмотрении симплициальных схем; поэтому алгебраическая Т. иногда и до сих пор называется комбинаторной Т. Вводятся пространства близости и равномерные пространства. Начинает интенсивно развиваться теория гомотопий (Х. Хопф , Понтрягин); определяются гомотопические группы (В. Гуревич, США) и для их вычисления применяются соображения гладкой Т. (Понтрягин). Формулируются аксиомы групп гомологий и когомологий (Н. Стинрод и С. Эйленберг, США). Возникает теория расслоений (Х. Уитни, США; Понтрягин); вводятся клеточные пространства (Дж. Уайтхед, Великобритания). Во 2-й половине 20 в. в СССР складывается советская школа общей Т. и теории гомологий: ведутся работы по теории размерности, проблеме метризации, теории (би)компактных расширений, общей теории непрерывных отображений (факторных, открытых, замкнутых), в частности теории абсолютов; теории так называемых кардинальнозначных инвариантов (А.В. Архангельский, Б. А. Пасынков, В. И. Пономарев, Е. Г. Скляренко, Ю. М. Смирнов и др.). Усилиями ряда учёных (Ж. П. Серр и А. Картан во Франции, М. М. Постников в СССР, Уайтхед и др.) окончательно складывается теория гомотопий. В это время создаются крупные центры алгебраической Т. в США, Великобритании и др. странах; возобновляется интерес к геометрической Т. Создаётся теория векторных расслоений и К-функтора (М. Атья, Великобритания; Ф. Хирцебрух, ФРГ), алгебраическая Т. получает широкие применения в гладкой Т. (Р. Том, Франция) и алгебраической геометрии (Хирцебрух); развивается теория (ко)бордизмов (В. А. Рохлин, СССР; Том, С. П. Новиков ) и теория сглаживания и триангулируемости (Дж. Милнор, США). Развитие Т. продолжается во всех направлениях, а сфера её приложений непрерывно расширяется. А. А. Мальцев. Лит.:Александров П. С., Введение в общую теорию множеств и функций, М.-Л., 1948; Пархоменко А. С., Что такое линия, М., 1954; Понтрягин Л. С., Основы комбинаторной топологии, М.-Л., 1947; его же, Непрерывные группы, 3 изд., М., 1973; Милнор Дж., Уоллес А,, Дифференциальная топология. Начальный курс, пер. с англ., М., 1972; Стинрод Н., Чинн У., Первые понятия топологии, пер. с англ., М., 1967; Александров П. С., Комбинаторная топология, М.-Л., 1947; Александров П. С., Пасынков Б. А., Введение в теорию размерности. Введение в теорию топологических пространств и общую теорию размерности, М., 1973; Александров П. С., Введение в гомологическую теорию размерности и общую комбинаторную топологию, М., 1975; Архангельский А. В., Пономарев В. И,, Основы общей топологии в задачах и упражнениях, М., 1974; Постников М. М., Введение в теорию Морса, М., 1971; Бурбаки Н., Общая топология. Основные структуры, пер. с франц., М., 1968; его же, Общая топология. Топологические группы. Числа и связанные с ними группы и пространства, пер. с франц., М., 1969; его же, Общая топология. Использование вещественных чисел в общей топологии. Функциональные пространства. Сводка результатов. Словарь, пер. с франц., М., 1975; Куратовский К., Топология, пер. с англ., т. 1-2, М., 1966-69; Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; Спеньер Э., Алгебраическая топология, пер. с англ., М., 1971. М. М. Постников. Тополь То'поль(Populus), род растений семейства ивовых. Двудомные листопадные деревья высотой до 40-45 ми диаметром до 1 ми больше. Листья очередные, черешчатые, различные по форме. Цветки в пазухах прицветников, зубчатых или рассеченных на нитевидные доли, состоят из диска бокало- или блюдцевидной формы и сидящего на нём пестика (у пестичных цветков) или многочисленных тычинок (у тычиночных цветков); собраны в поникающие серёжки, появляющиеся до распускания листьев или одновременно с ними; опыление ветром. Плод - коробочка с многочисленными мелкими волосистыми семенами, разносимыми ветром. Свыше 100 видов (по др. данным, 35-40), преимущественно в умеренном поясе Северном полушария, на юге - до Танганьики, Уганды и Севера Мексики. В СССР около 30 видов, 12 видов интродуцировано. Многие виды Т. декоративны, быстро растут, отличаются высокой способностью к вегетативному размножению черенками и корневыми отпрысками и поэтому часто используются в озеленении. Разводят: Т. бальзамический (P. balsamifera), Т. белый (P. alba), Т. душистый (P. suaveolens), Т. канадский (P. deltoides), осокорь , осину , Т. пирамидальный (P. pyramidalis) и др. виды и гибриды. Древесина лёгкая, белая, мягкая, применяется в спичечном и бумажном производстве, в строительстве, идёт на изготовление фанеры, тары и т.д. Лит.:Деревья и кустарники СССР, т. 2, М. - Л., 1951. В. Н. Гладкова. 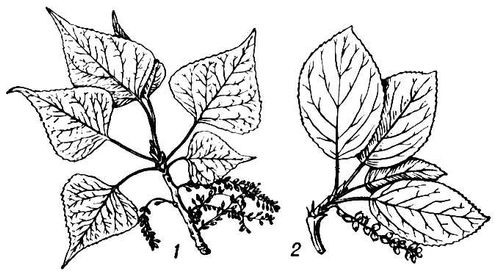
Ветви с плодами тополя: 1 - чёрного, или осокоря; 2 - душистого. Топольные озёра То'польные озёра,Большое и Малое, озёра в Кулундинской степи, в низовье р. Бурла. Большое Топольное озеро расположено на высоте 98 м.Площадь 76,6 км 2, средняя глубина 2,1 м, наибольшая 2,4 м.Южный берег заболочен. Питание в основном снеговое. В 1966 сток из Большого Топольного озера зарегулирован плотиной при выходе. Рыборазведение и рыболовство. Малое Топольное озеро расположено северо-восточнее Большого Топольного. Площадь 13,6 км 2, бессточное, зарастающее. Топоморфоз Топоморфо'з(от греч. tо'pos - место и morph - вид, форма), принцип эволюционных преобразований органов, при котором в процессе филогенеза данной группы организмов у особей происходит изменение положения целого органа или отдельных его частей. Топонимика Топони'мика(от греч. tо'pos - место и о'nyma - имя, название), составная часть ономастики , изучающая географические названия (топонимы), их значение, структуру, происхождение и ареал распространения. Совокупность топонимов на какой-либо территории составляет её топонимию. Микротопонимия включает названия небольших географических объектов: урочищ, ключей, омутов, с.-х. угодий и т.п. Т. развивается в тесном взаимодействии с географией, историей, этнографией. Топонимия - важный источник для исследования истории языка (истории лексикологии, диалектологии, этимологии и др.), так как некоторые топонимы (особенно гидронимы) устойчиво сохраняют архаизмы и диалектизмы, часто восходят к языкам- субстратам народов, живших на данной территории Т. помогает восстановить черты исторического прошлого народов, определить границы их расселения, очертить области былого распространения языков, географию культурных и экономических центров, торговых путей и т.п. Прикладным аспектом Т. является практическая транскрипция топонимов, устанавливающая их исходное и единообразное написание и передачу на др. языках, что важно для картографирования военных целей и всех видов коммуникации. Лит.:Никонов В. А., Введение в топонимику, М., 1965; ПоповА. И., Географические названия, М. - Л., 1965; Жучкевич В. А., Общая топонимика, 2 изд., Минск, 1968; Поспелов Е. М., Топонимика и картография, М., 1971; Мурзаев Э. М., Очерки топонимики, М., 1974. В. П. Нерознак. Топор Топо'р,рубящее орудие, предназначенное главным образом для обработки дерева; применялся и как оружие. Появился в раннем неолите, имел вид вытянутого каменного клина, закреплявшегося в расщепленном конце деревянной рукояти. В позднем неолите и бронзовом веке распространились полированные каменные Т. В эпоху бронзы появились также медные и бронзовые проушные Т. (с отверстием для рукояти). Каменные Т. после этого тоже стали делать проушными, повторяющими по форме металлические (воспроизводился даже литейный шов). В железном веке повсеместно распространились железные проушные Т. В Древней Руси 11-13 вв. различались Т. лесорубные, плотничные и боевые (последние часто богато украшались). Современный тип Т. распространился с начале 17 в. Топорик Топо'рик(Lunda cirrhata), птица семейства чистиковых. Длина около 40 см, весит 600-800 г. Мощный высокий клюв сильно сжат с боков. Окраска черно-бурая, щёки белые, за глазами пучки длинных желтоватых перьев. Лапы красные. Хорошо ходит, летает, плавает и ныряет. Питается мелкой рыбой и морскими беспозвоночными. Единственное яйцо откладывает в нору (которую роет в мягком грунте) или под камнями. Вылупившийся птенец покрыт густым длинным и тонким пухом; покидает гнездо полностью оперившись. Т. гнездятся колониями по побережьям северной части Тихого океана Местами служат объектом промысла (в пищу используются мясо и яйца). 
Рис. к ст. Топорик. Топорков Василий Осипович Топорко'вВасилий Осипович [4(16).3.1889, Петербург, - 25.8.1970, Москва], русский советский актёр, народный артист СССР (1948), доктор искусствоведения (1965). В 1909 окончил Петербургское театральное училище. Работал в Петербургском театре Литературно-художественного общества, затем в московском большом Театре Корша, с 1927 во МХАТе, где подготовил под руководством К. С. Станиславского роли - Ванечки в «Растратчиках» Катаева и Чичикова в «Мёртвых душах» по Гоголю. Т. - один из последовательных учеников Станиславского и пропагандистов его системы. Создал остро сатирические образы Оргона («Тартюф» Мольера), Кругосветлова («Плоды просвещения» Л. Н. Толстого). Ряд его ролей носил жизнеутверждающий характер - Берест («Платон Кречет» Корнейчука), Морис («Глубокая разведка» Крона) и др. В творчестве Т. точность социального анализа и тонкость психологических характеристик сочетались с глубокой эмоциональной насыщенностью. Актёр умел удивительно рельефно передавать душевный перелом героя - Мышлаевский, Битков («Дни Турбиных», «Последние дни» Булгакова) и др. Автор книг и статей об учении Станиславского («Станиславский на репетиции», М. - Л., 1949, и др.). Преподавал в Школе-студии им. Вл. И. Немировича-Данченко (с 1948 профессор). Государственные премии СССР (1946, 1952). Награжден 2 орденами, а также медалями. Лит.:Рогачевский М. Л., В. О. Топорков, М., 1969. Ю. Я. Зубков. 
В. О. Топорков. Топоскоп Топоско'п(от греч. tо'pos - место и skopе'M - смотрю), прибор, демонстрирующий мгновенное распределение уровней биоэлектрических потенциалов в нескольких десятках точек организма в виде группы пятен измененной яркости свечения экрана кинескопа. Положение этих пятен на экране соответствует расположению отводящих электродов на теле животного или человека. Регистрация кинокамерой показаний Т. позволяет судить о динамике изменений изучаемых потенциалов во времени. Электроэнцефалоскопы дают возможность увеличить количество пунктов исследований биоэлектрической активности мозга до 50-100. Подробнее см. Электроэнцефалография . Лит.:Ливанов М. Н., Ананьев В. М., Электроэнцефалоскопия, М., 1959; Амиров Р. 3., Интегральные топограммы потенциалов сердца, М., 1973. Топохимические реакции Топохими'ческие реа'кции, реакции химические , происходящие на границе раздела твёрдых фаз. Примеры Т. р.: дегидратация кристаллогидратов, восстановление окислов, термический распад азидов тяжёлых металлов и т.д. Особенности Т. р.: 1) они начинаются не во всём объёме, а с отдельных, наиболее реакционноспособных мест твёрдого тела (локализация процесса); 2) возникнув в каком-то месте, реакция продолжается в соседних областях кристалла (автолокализация процесса). Причины локализации процесса при Т. р. обычно связаны с наличием дефектов в кристаллах и малой подвижностью ионов, атомов или молекул, образующих кристаллическую решётку . Автолокализация процесса обусловлена каталитическим влиянием твёрдого или газообразного продукта реакции, а также кристаллохимическими особенностями развития реакции в кристалле. Межфазовая поверхность, в пределах которой локализованы Т. р., возникает вследствие образования и роста реакционных ядер; скорость процесса обычно пропорциональна величине этой поверхности в каждый данный момент времени. Поэтому кинетический анализ Т. р. включает не только учёт развития процесса во времени, но и в пространстве. Значит, влияние на скорость Т. р. оказывают дефекты в кристаллах. Оно проявляется в изменении как числа потенциальных центров реакции на поверхности, так и условий для явлений переноса в твёрдом теле. С существенной ролью дефектов в развитии Т. р. связаны также широко известный эффект влияния «предыстории» препарата (реагента) на его реакционную способность, многообразие факторов, воздействующих на их скорость, и т.д. Характер влияния дефектов в кристаллах на скорости Т. р. в каждом конкретном случае зависит как от вида и концентрации дефектов, так и от механизма элементарных стадий. Т. р. широко используются на практике. К числу наиболее важных Т. р. относятся процессы обжига, восстановления, хлорирования руд многих металлов, цементация стали, производство керамики и огнеупоров, приготовление катализаторов, получение ферритов, некоторые стадии фотографического процесса, газовая коррозия металлов и сплавов. Во многих случаях разложение взрывчатых веществ при нагревании, процессы синтеза и очистки полупроводниковых материалов также относятся к Т. р. Лит.:Болдырев В. В., Влияние дефектов в кристаллах на скорость термического разложения твердых веществ, Томск, 1963; Дельмон Б., Кинетика гетерогенных реакций, пер. с франц., М., 1972; Розовский А. Я., Кинетика топохимических реакций, М., 1974. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36 |
|||||||
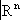 , не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при
N³
2
n+ 1). Аналогичный результат верен и при a
=
t,
p.
, не имеющие особых точек. Оказывается (теорема вложения), что любое гладкое многообразие диффеоморфно такой поверхности (при
N³
2
n+ 1). Аналогичный результат верен и при a
=
t,
p. (некомпактное многообразие). Для любого a
=
p,
sна
t-многообразиях
S
1и
(некомпактное многообразие). Для любого a
=
p,
sна
t-многообразиях
S
1и
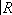 существует единственная a-структура.
существует единственная a-структура.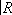 P
2# ¼ #
P
2# ¼ #
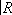 P
2некоторого числа проективных плоскостей
P
2некоторого числа проективных плоскостей
 P
2. Её можно представлять себе как сферу, к которой приклеено несколько
Мебиуса листов
.
P
2. Её можно представлять себе как сферу, к которой приклеено несколько
Мебиуса листов
.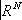 ; и касательные векторы к
Хсоставляют некоторое новое гладкое многообразие
TX,которое называется касательным расслоением гладкого многообразия
X. Вообще, векторным расслоением над топологическим пространством
Хназывается топологическое пространство
Е,для которого задано такое непрерывное отображение p :
Е®
Х, что для каждой точки
хО
Хпрообраз v (слой) является векторным пространством и существует такое открытое покрытие {
U
a} пространства
X, что для любого a прообраз p
-1(
U
a) гомеоморфен произведению
U
aґ
; и касательные векторы к
Хсоставляют некоторое новое гладкое многообразие
TX,которое называется касательным расслоением гладкого многообразия
X. Вообще, векторным расслоением над топологическим пространством
Хназывается топологическое пространство
Е,для которого задано такое непрерывное отображение p :
Е®
Х, что для каждой точки
хО
Хпрообраз v (слой) является векторным пространством и существует такое открытое покрытие {
U
a} пространства
X, что для любого a прообраз p
-1(
U
a) гомеоморфен произведению
U
aґ
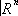 , причём существует гомеоморфизм p
-1(
U
a) ®
U
aґ
, причём существует гомеоморфизм p
-1(
U
a) ®
U
aґ
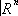 , линейно отображающий каждый слой p
-1
(x), xО
U
a
,на векторное пространство
{х}ґ
, линейно отображающий каждый слой p
-1
(x), xО
U
a
,на векторное пространство
{х}ґ
 . При
Е=
TXнепрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p
-1
(x)будет пространство, касательное к
Хв точке
х.Оказывается, что любое векторное расслоение над компактным пространством
Хопределяет некоторый элемент группы
KO(X).Таким образом, в частности, для любого гладкого, компактного и связного многообразия
Хв группе
KO(X)определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия
X. Имеется аналог этой конструкции для любого a. При a =
pроль группы
KO(X)играет некоторая другая группа, которая обозначается
KPL(X),а при a =
tроль этой группы играет группа, обозначаемая
KTop(X).Каждое a-многообразие
Хопределяет в соответствующей группе [
КО(Х),
KPL(X)или
KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы
KO(X)®
KPL(X)®
KTop(X), и оказывается, что на
n-мерном (
n³
5) компактном и связном a'-многообразии
X, где a' =
t,
p, тогда и только тогда можно ввести a-структуру (a =
р,если a'
= t,и a =
s,если a' =
p)
,когда его a'-тангенциальный инвариант лежит в образе соответствующей группы [
KPL(X)при a' =
tи
KO(X)при a' =
p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [
X,
Y
a], где
Y
a- некоторое специальным образом сконструированное топологическое пространство (при a =
sтопологическое пространство
Y
aобозначается обычно символом
PL/O, а при a =
p -символом
Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства
PL/Oдовольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что p
i(
PL/O)
= 0 при
iЈ 6, откуда следует, что любое кусочно-линейное многообразие размерности
nЈ 7 сглаживаемо, а при
nЈ 6 единственным образом. Напротив, гомотопический тип топологического пространства
Top/PLоказался удивительно простым: это пространство гомотопически эквивалентно
K($
2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы
H
3(
X, $
2). Такие структуры заведомо существуют, если
H
4(
X, $
2) = 0, но при
H
4(
X, $
2) ¹ 0 кусочно-линейной структуры может не существовать.
. При
Е=
TXнепрерывное отображение p сопоставляет с каждым касательным вектором точку его касания, так что слоем p
-1
(x)будет пространство, касательное к
Хв точке
х.Оказывается, что любое векторное расслоение над компактным пространством
Хопределяет некоторый элемент группы
KO(X).Таким образом, в частности, для любого гладкого, компактного и связного многообразия
Хв группе
KO(X)определён элемент, соответствующий касательному расслоению. Он называется тангенциальным инвариантом гладкого многообразия
X. Имеется аналог этой конструкции для любого a. При a =
pроль группы
KO(X)играет некоторая другая группа, которая обозначается
KPL(X),а при a =
tроль этой группы играет группа, обозначаемая
KTop(X).Каждое a-многообразие
Хопределяет в соответствующей группе [
КО(Х),
KPL(X)или
KTop(X)] некоторый элемент, называемый его a-тангенциальным инвариантом. Имеются естественные гомоморфизмы
KO(X)®
KPL(X)®
KTop(X), и оказывается, что на
n-мерном (
n³
5) компактном и связном a'-многообразии
X, где a' =
t,
p, тогда и только тогда можно ввести a-структуру (a =
р,если a'
= t,и a =
s,если a' =
p)
,когда его a'-тангенциальный инвариант лежит в образе соответствующей группы [
KPL(X)при a' =
tи
KO(X)при a' =
p]. Число таких структур конечно и равно числу элементов некоторого фактормножества множества [
X,
Y
a], где
Y
a- некоторое специальным образом сконструированное топологическое пространство (при a =
sтопологическое пространство
Y
aобозначается обычно символом
PL/O, а при a =
p -символом
Top/PL). Тем самым вопрос о существовании и единственности a-структуры сводится к некоторой задаче теории гомотопий. Гомотопический тип топологического пространства
PL/Oдовольно сложен и до сих пор (1976) полностью не вычислен; однако известно, что p
i(
PL/O)
= 0 при
iЈ 6, откуда следует, что любое кусочно-линейное многообразие размерности
nЈ 7 сглаживаемо, а при
nЈ 6 единственным образом. Напротив, гомотопический тип топологического пространства
Top/PLоказался удивительно простым: это пространство гомотопически эквивалентно
K($
2, 3). Следовательно, число кусочно-линейных структур на топологическом многообразии не превосходит числа элементов группы
H
3(
X, $
2). Такие структуры заведомо существуют, если
H
4(
X, $
2) = 0, но при
H
4(
X, $
2) ¹ 0 кусочно-линейной структуры может не существовать.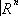 . Край является (
n-1)-мерным a-многообразием (вообще говоря, несвязным). Два
n-мерных компактных a-многообразия
Хи
Yназываются (ко) бордантными, если существует такое (
n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных
Хи
У. Если отображения вложения
X®
Wи
Y®
Wявляются гомотопическими эквивалентностями, то гладкие многообразия называются
h-кобордантными. Методами разложения на ручки удаётся доказать, что при
n³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они
h-кобордантны. Эта теорема о
h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.
. Край является (
n-1)-мерным a-многообразием (вообще говоря, несвязным). Два
n-мерных компактных a-многообразия
Хи
Yназываются (ко) бордантными, если существует такое (
n+1)-мерное компактное a-многообразие с краем W, что его край является объединением непересекающихся гладких многообразий, a-гомеоморфных
Хи
У. Если отображения вложения
X®
Wи
Y®
Wявляются гомотопическими эквивалентностями, то гладкие многообразия называются
h-кобордантными. Методами разложения на ручки удаётся доказать, что при
n³ 5 односвязные компактные a-многоооразия a-гомеоморфны, если они
h-кобордантны. Эта теорема о
h-кобордизме доставляет сильнейший способ установления a-гомеоморфности a-многообразий (в частности, гипотеза Пуанкаре является её следствием). Аналогичный, но более сложный результат имеет место и для неодносвязных a-многообразий.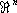 классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a =
sизоморфна гомотопической группе p
2n+1
MO(
n+1) некоторого специально сконструированного топологического пространства
MO(
n+1), называется пространством Тома. Аналогичный результат имеет место и при a =
p,
t. Поэтому методы алгебраической Т. позволяют в принципе вычислить группу
классов кобордантных компактных a-многообразий является по отношению к операции связной суммы коммутативной группой. Нулём этой группы служит класс a-многообразий, являющихся краями, то есть кобордантных нулю. Оказывается, что эта группа при a =
sизоморфна гомотопической группе p
2n+1
MO(
n+1) некоторого специально сконструированного топологического пространства
MO(
n+1), называется пространством Тома. Аналогичный результат имеет место и при a =
p,
t. Поэтому методы алгебраической Т. позволяют в принципе вычислить группу
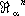 .В частности, оказывается, что группа
.В частности, оказывается, что группа
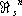 является прямой суммой групп $
2в количестве, равном числу разбиений числа
nна слагаемые, отличные от чисел вида 2
m-1. Например,
является прямой суммой групп $
2в количестве, равном числу разбиений числа
nна слагаемые, отличные от чисел вида 2
m-1. Например,
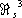 =0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив,
=0 (так что каждое трёхмерное компактное гладкое многообразие является краем). Напротив,
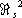 = $
2
,так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость
= $
2
,так что существуют поверхности, кобордантные друг другу и не кобордантные нулю; такой поверхностью, например, является проективная плоскость
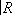 P
2.
P
2.