Функциональный определитель
Функциона'льный определи'тель,определитель, элементами которого являются функции одного или многих переменных. Наиболее важные примеры Ф. о. —
, играющий важную роль в теории линейных дифференциальных уравнений высшего порядка, гессиан, применяемый в теории алгебраических кривых, и
, используемый при преобразовании кратных интегралов, установлении независимости системы функций и др. вопросах теории функций многих переменных. Производная Ф. о.
D(
x) = |
a
ik(
x)|
n-го порядка равна сумме
nФ. о., матрицы которых получаются из матрицы ||
a
ik(
x)|| соответственно дифференцированием элементов первого, второго,...,
n-го столбца. Например, если
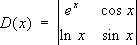
,
то
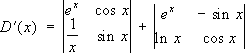
.
Иногда термин «Ф. о.» применяется для обозначения якобиана.
Функция (в языкознании)
Фу'нкцияв языкознании, способность языковой формы к выполнению того или иного назначения (нередко синоним терминам «значение» и «назначение» языковой формы); зависимость или отношения между единицами языка, обнаруживаемые на всех уровнях его системы. Установление Ф. языковой единицы предполагает определение её роли в данном языке (системе языка), например у предложения могут быть выделены коммуникативная (сообщать о чём-то) и номинативная (называть это событие) Ф. Каждая языковая единица существует исключительно потому, что она, в отличие от др. языковой единицы, служит известной цели, т. е. выполняет определённую Ф. Выделяются многочисленные Ф. языковых единиц — отождествления, разграничения и различения, в соответствии с которыми различаются и сами единицы, например
служит различению разных слов и
или проведению границ между ними.
Ф. изучаются и рассматриваются не только при описании единиц языка, но и самого языка как системы. Основная Ф. языка: коммуникативная, или Ф. общения, познавательная, отражательная, перформативная, фатическая (установление контакта без установки на передачу информации), номинативная — наречение или называние предметов и явлений действительности, экспрессивная, или Ф. выражения, аппелятивная, или Ф. обращения. В числе Ф. языка указывают также на уровневые Ф. — фонологические, морфологические, грамматические и др. С функциональной точки зрения система языка есть многомерное образование, дифференцируемое как по формам проявления (устный и письменный язык), так и по социальной предназначенности (литературный язык, социальные диалекты, арго и пр.), по эстетической направленности (поэтический язык), по конкретным задачам общения (специальные терминологические системы).
Е. С. Кубрякова.
Функция (математ.)
Фу'нкция,одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Если величины
xи
усвязаны так, что каждому значению
xсоответствует определённое значение
у, то
уназывают (однозначной) функцией аргумента
x. Иногда
xназывают независимой, а
у— зависимой переменной. Записывают указанное соотношение между
xи
ув общем виде так:
у=
f(
x) или
у=
F(
x) и т. п. Если связь между
xи
утакова, что одному и тому же значению
xсоответствует вообще несколько (быть может даже бесконечное множество) значений
у, то
уназывают многозначной Ф. аргумента
x. Задать Ф.
у=
f(
x) значит указать:
1) множество
Азначений, которые может принимать
x(область задания Ф.),
2) множество
Взначений, которые может принимать
у(область значения Ф.), и
3) правило, по которому значениям
xиз
Асоотносятся значения
уиз
В. В простейших случаях областью задания Ф. служит вся числовая прямая или её отрезок
аЈ
xЈ
b(или интервал
а<
x<
b).
Правило отнесения значениям
xсоответствующих им значений
учаще всего задаётся формулой, устанавливающей, какие вычислительные операции надо произвести над
x, чтобы найти
у. Таковы, например, формулы
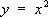
,

и т. п. К вычислительным (или аналитическим) операциям, кроме четырёх действий арифметики, принято относить также операцию перехода к пределу (т. е. нахождение по заданной последовательности чисел
a
1,
a
2,
a
3,... её
lim
a
n, если он существует), хотя никаких общих способов производства этой операции нет. В 1905 А.
предложил общее определение аналитически изобразимой Ф. как Ф., значения которой получаются из значений
xи постоянных величин при помощи арифметических действий и предельных переходов. Все т. н. элементарные Ф. sin
x, cos
x,
a
x,
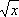
, log
x, arctg
xи т. п. аналитически изобразимы. Например, cos
xпредставляется формулой:
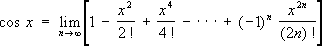
.
В 1885 К.
установил аналитическую изобразимость любой
. Именно, он показал, что всякая Ф., непрерывная на каком-нибудь отрезке, является пределом последовательности многочленов вида
c
0+
c
1x+
c
2x
2+...+
c
nx
n.
Кроме описанного здесь аналитического способа задания Ф. при помощи формулы, применяются и др. способы. Так, в тригонометрии Ф. cos
xопределяется как проекция единичного вектора на ось, образующую с ним угол в
xрадианов, а Ф.
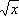
в алгебре как число, квадрат которого равен
x. Возможность задания этих Ф. при помощи аналитических формул устанавливается лишь при более углублённом их изучении. Упомянем ещё о т. н. функции Дирихле y(
x), равной 1, если
x— число рациональное, и 0, если
x— число иррациональное. Впервые эта Ф. была введена этим «бесформульным» способом, но впоследствии для неё была найдена и аналитическая формула:
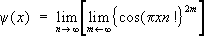
.
Существуют, однако, и такие Ф., которые не представимы в описанном выше смысле никакой аналитической формулой. Такими Ф., во всяком случае, являются т. н. неизмеримые по Лебегу Ф.
К Ф., заданным одной аналитической формулой, примыкают Ф., которые на разных частях своей области задания определены различными формулами. Такова, например, Ф.
f(
x), заданная так:
f(
x) =
x, если
xЈ 1, и
f(
x) =
x
2, если
x> 1. Приведённое выше «бесформульное» задание функции Дирихле y(
x) также принадлежит к этому типу.
Ф.
y=
f(
x) иногда задаётся своим графиком, т. е. множеством тех точек (
x,
у) плоскости, у которых
xпринадлежит области задания Ф., а
у=
f(
x). В прикладных вопросах часто довольствуются таким заданием Ф., когда её график просто начерчен на плоскости (
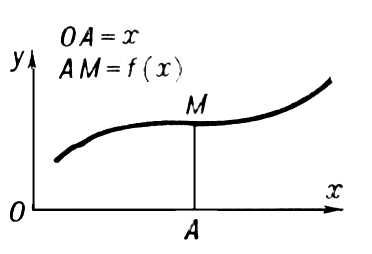
рис.
), а значения Ф. снимаются с чертежа. Так, например, верхние слои атмосферы можно изучать при помощи шаров-зондов, несущих самопишущие приборы, непосредственно доставляющие кривые изменения температуры, давления и т. п.
Чтобы задание Ф. графиком было вполне корректным с чисто математической точки зрения, недостаточно, однако, просто начертить её график, ибо задание геометрического объекта чертежом всегда недостаточно определенно. Поэтому для графического задания Ф. должна быть указана точная геометрическая конструкция её графика. Чаще всего эта конструкция задаётся при помощи уравнения, что возвращает нас к аналитическому заданию Ф., однако возможны и чисто геометрические методы построения графика (например, прямая линия вполне определяется заданием координат двух её точек).
В технике и естествознании часто встречается следующая ситуация: зависимость между величинами
xи
узаведомо существует, но неизвестна. Тогда производят ряд экспериментов, в каждом из которых удаётся измерить одно из значений величины
xи соответствующее ему значение
у. В результате составляется более или менее обширная таблица, сопоставляющая измеренным значениям
xсоответствующие значения
у. Тогда говорят о «табличном» задании Ф. Нахождение для такой Ф. аналитической формулы (см.
) не раз представляло собой важное научное открытие (например, открытие Р.
и Э.
формулы
pv=
С, связывающей давление и объём массы газа). Табличное задание Ф. с чисто математической точки зрения вполне корректно, если под областью задания Ф. понимать именно то множество значений
x, которое внесено в таблицу, и табличные значения
усчитать абсолютно точными. Кроме Ф. одного аргумента, о которых шла речь, в математике и её приложениях, большое значение имеют Ф. нескольких аргументов. Пусть, например, каждой системе значений трёх переменных
x,
у,
zсоответствует определённое значение четвёртой переменной
u. Тогда говорят, что
uесть (однозначная) Ф. аргументов
x,
у,
z, и пишут
u=
f(
x,
у,
z). Формулы
u=
x+ 2
y,
u= (
x+
у) sin
zдают примеры аналитического задания Ф. двух и трёх аргументов. Аналогично определяются и многозначные Ф. нескольких аргументов. Ф. двух аргументов
z=
f(
x,
y) можно задать и при помощи её графика, т. е. множества точек (
x,
у,
z) пространства, у которых (
x,
у) принадлежит области задания Ф., а
z=
f(
x,
у). В простейших случаях таким графиком служит некоторая поверхность.
Развитие математики в 19 и 20 вв. привело к необходимости дальнейшего обобщения понятия Ф., заключавшегося в перенесении этого понятия с переменных действительных чисел сначала на переменные комплексные числа, а затем и на переменные математические объекты любой природы. Например, если каждому кругу
xплоскости соотнести его площадь
у, то
убудет функцией
x, хотя
xуже не число, а геометрическая фигура. Точно так же, если каждому шару
xтрёхмерного пространства соотнести его центр
у, то здесь уже ни
x, ни
yне будут числами.
Общее определение однозначной Ф. можно сформулировать так: пусть
А= {
x} и
В= {
у} — два непустых множества, составленных из элементов любой природы, и
М— множество упорядоченных пар (
x,
у) (где
xО
А,
уО
В) такое, что каждый элемент
xО
Авходит в одну и только одну пару из
М; тогда
Мзадаёт на
Афункцию
y=
f(
x), значение которой для каждого отдельного
x
0О
Аесть элемент
y
0О
В, входящий в единственную пару из
М, имеющую
x
0своим первым элементом.
При указанном расширении понятия Ф. стирается различие между Ф. одного и нескольких аргументов. Например, всякую Ф. трёх числовых переменных
x,
у,
zможно считать Ф. одного аргумента — точки (
x,
у,
z) трёхмерного пространства. Более того, такие обобщения понятия Ф., как функционал или оператор (см.
), также охватываются приведённым определением.
Как и остальные понятия математики, понятие Ф. сложилось не сразу, а прошло долгий путь развития. В работе П.
«Введение и изучение плоских и телесных мест» говорится: «Всякий раз, когда в заключительном уравнении имеются две неизвестных величины, налицо имеется место». По существу здесь идёт речь о функциональной зависимости и её графическом изображении («место» у Ферма означает линию). Изучение линий по их уравнениям в «Геометрии» Р.
(1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У И.
(«Лекции по геометрии», 1670) в геометрической форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует уже о совершенно отчётливом владении понятием Ф. В геометрическом и механическом виде это понятие мы находим и у И.
, Однако термин «Ф.» впервые появляется лишь в 1692 у Г.
и притом не совсем в современном понимании его. Лейбниц называет Ф. различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек и т. п.). В первом печатном курсе «Анализа бесконечно малых» Г.
(1696) термин «Ф.» не употреблялся.
Первое определение Ф. в смысле, близком к современному, встречается у И.
(1718): «Функция это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания Ф. аналитической формулой. Та же идея выступает и в определении Л.
(см. «Введение в анализ бесконечных», 1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств». Впрочем, уже Эйлеру было не чуждо и современное понимание Ф., которое не связывает понятие Ф. с каким-либо аналитическим её выражением. В его «Дифференциальном исчислении» (1755) говорится: «Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых». Всё же в 18 в. отсутствовало достаточно ясное понимание различия между Ф. и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Д.
(1753). В основе решения Бернулли лежало утверждение о возможности разложить любую Ф. в тригонометрический ряд. Возражая против этого, Эйлер указал
на то, что подобная разложимость доставляла бы для любой Ф. аналитическое выражение, в то время как Ф. может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»). Эта критика убедительна и с современной точки зрения, ибо не все Ф. допускают аналитическое изображение (правда, у Бернулли речь идёт о непрерывной Ф., которая всегда аналитически изобразима, но она может и не разлагаться в тригонометрический ряд). Однако другие аргументы Эйлера уже ошибочны. Например, Эйлер считал, что разложение Ф. в тригонометрический ряд доставляет для неё единое аналитическое выражение, в то время как она может быть «смешанной» Ф., представимой на разных отрезках разными формулами. На самом деле одно другому не противоречит, но в ту эпоху казалось невозможным, чтобы два аналитических выражения, совпадая на части отрезка, не совпадали на всём его протяжении.
Эти ошибочные взгляды мешали развитию теории тригонометрических рядов, и лишь в работах Ж.
(1822) и П.
(1829) правильные по существу идеи Д. Бернулли получили дальнейшее развитие.
С начала 19 в. уже всё чаще и чаще определяют понятие Ф. без упоминания об её аналитическом изображении. В руководстве французского математика С. Лакруа (1810) говорится: «Всякая величина, значение которой зависит от одной или многих других величин, называется функцией этих последних». В «Аналитической теории тепла» Ж. Фурье (1822) имеется фраза: «Функция
fxобозначает функцию совершенно произвольную, т. е. последовательность данных значений, подчиненных или нет общему закону и соответствующих всем значениям
x, содержащимся между 0 и какой-либо величиной
X». Близко к современному и определение Н. И.
(«Об исчезании тригонометрических строк», 1834):»... Общее понятие требует, чтобы функцией от
xназывать число, которое дается для каждого
xи вместе с
xпостепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной». Там же немного ниже сказано: «Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа одни с другими в связи, понимать как бы данными вместе». Т. о., современное определение Ф., свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле и высказанное в 1837, неоднократно предлагалось и до него.
В заключение отметим следующее важное открытие, принадлежащее Д. Е.
: всякая конечная измеримая (по Лебегу) на отрезке Ф. (см.
) разлагается в тригонометрический ряд, сходящийся к ней почти всюду. Т. к. обычно встречаемые Ф. измеримы, то можно сказать, что практически всякая Ф. изобразима аналитически с точностью до множества меры нуль.
Лит.:Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1—2, М., 1971—73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1—2, М., 1973; Никольский С. М., Курс математического анализа, 2 изд., т. 1—2, М.,1975
И. П. Натансон.
Рис. к ст. Функция.
Функция передачи модуляции
Фу'нкция переда'чи модуля'ции,то же, что и
.
Функция распределения
Фу'нкция распределе'ния,основное понятие
; характеризует плотность вероятности распределения частиц статистической системы по
(т. е. по координатам (
q
iи импульсам
p
i) в классической статистической физике или вероятность распределения по квантовомеханическим состояниям в квантовой статистике.
В классической статистической физике Ф. р.
f(
p,
q,
t) определяет вероятность
dw =
f(
p,
q,
t)
dp dqобнаружить систему из
Nчастиц в момент времени
tв элементе фазового объёма
dpdq=
dp
1dq
1...
dp
N
ґ
dq
N
вблизи точки
p
1,
q
1,...,
p
N,
q
n. Учитывая, что перестановка тождественных (одинаковых) частиц не меняет состояния, следует уменьшить фазовый объём в
N! раз; кроме того, удобно перейти к безразмерному элементу (Базового объёма, заменив
dpdqна
dpdq/N!
h
3N, где
hопределяет минимальный размер ячейки в фазовом пространстве. См. также
.
Функция (филос.)
Фу'нкция(от лат. functio — совершение, исполнение) (философская), отношение двух (группы) объектов, в котором изменение одного из них ведёт к изменению другого. Ф. может рассматриваться с точки зрения следствий (благоприятных, неблагоприятных — дисфункциональных или нейтральных — афункциональных), вызываемых изменением одного параметра в др. параметрах объекта (функциональность), или взаимосвязи отдельных частей в рамках некоторого целого (функционирование).
Понятие Ф. введено в научный оборот Г.
. В дальнейшем в философии интерес к Ф. как одной из фундаментальных категорий возрастал по мере распространения в различных областях науки функциональных методов исследования. В наиболее развёрнутой форме функциональный подход был реализован Э.
, который разработал теорию понятий, или «функций». Эта попытка построения теории познания на основе функционального подхода оказала определённое влияние на философские представления о Ф. Исследуются проблемы обоснованности, приемлемости и доказательности функциональных высказываний и объяснений, широко используемых в биологических и социальных науках, особенно в связи с изучением целенаправленных систем. См. также статьи
,
и лит. при них.
Лит.:Кассирер Э., Познание и действительность. Понятие о субстанции и понятие о функции, СПБ, 1912; Юдин Б. Г., Системные представления в функциональном подходе, в сборнике: Системные исследования. Ежегодник 1973, М., 1973, с. 108—26; Frege G., Funktion und Begriff, Jena, 1891; Wright L., Functions, «Philosophical Review», 1973, v. 82, April, p. 139—68; Cummins R., Functional analysis, «The Journal of Philosophy», 1975, v. 72, № 20.
Б. Г. Юдин.
Функция в социологии.1) Роль, которую определённый социальный институт или частный социальный процесс выполняет относительно потребностей общественной системы более высокого уровня организации или интересов составляющих её классов, социальных групп и индивидов. Например, Ф. государства, семьи, искусства и т.д. относительно общества. При этом различаются явные Ф., т. е. совпадающие с открыто провозглашаемыми целями и задачами института или социальной группы, и скрытые, латентные Ф., обнаруживающие себя лишь с течением времени и отличающиеся от провозглашаемых намерений участников этой деятельности. 2) Зависимость, которая наблюдается между различными компонентами единого социального процесса, когда изменения одной части системы оказываются производными от изменений в другой её части (например, изменения в соотношении городского и сельского населения как Ф. развития промышленности).
Марксистский поход к исследованию функций опирается на классовый анализ как самих институтов, так и соответствующих потребностей и интересов. См. также статьи
,
и литература при них.
А. Г. Здравомыслов.
Фунт (денежная единица)
Фунт,денежная единица АРЕ (егип. Ф. = 100
= 1000
), Израиля (израильский Ф. = 100
), Ирландии (ирландский Ф. = 100 пенсам), Ливана, Сирии (ливанский, сирийский Ф. = 100 пиастрам), а также Кипра, Судана, Мальты, Гибралтара и некоторых др. стран. По курсу Госбанка СССР (сентябрь 1977) 100 сирийских Ф.= 18 руб. 82 коп. 1 египетский Ф. = 1 руб. 85 коп., 100 ливанских Ф. = 23 руб. 50 коп., 1 суданский Ф. = 2 руб. 14 коп.
Фунт (единица массы)
Фунт(польский funt, от немецкого Pfund, от латинского pondus — вес, тяжесть, гиря),
1) единица массы в русской системе мер, отмененной в 1918. 1 Ф. (торговый) =
1/
40
= 32 лотам = 96
= 9216 долям = 0,40951241
кг. Эталоном Ф. служил прототип, хранимый в
. В России применялся также аптекарский Ф., равный
7/
8торгового Ф., т. е. 0,35832336
кг(см.
).
2) Основная единица в системе
(обозначается 1 b). 1 Ф. (торговый) = 0,45359237
кг. Ф. подразделяется на 16 унций, на 16 ґ 16 = 256
, а также на 7000
. Кроме торгового Ф., в США, Великобритании и ряде др. стран применяются аптекарский и тройский (монетный) Ф., равные 0,37324177
кг.
Фунт стерлингов
Фунт сте'рлингов(англ. pound, или pound sterling), денежная единица Великобритании, делится на 100 пенсов (до февраля 1971 1 Ф. с. = 20
= 240 пенсам). С 11 в. чеканились монеты из серебра и с середины 14 в. также из золота. Выпуск банкнот в Ф. с. начат
с 1694. В 1816 в стране был введён золотомонетный стандарт (существовал до августа 1914): официальное золотое содержание Ф. с. установлено в 7322382
гчистого золота. С апреля 1925 по сентябрь 1931 действовал золотослитковый стандарт. После отмены золотого стандарта и прекращения размена банкнот на золото Ф. с. обесценился: его паритет к доллару США снизился с 4,86653 долл. до 3,5 долл. в 1932. В дальнейшем Ф. с. неоднократно девальвировался. В ноябре 1967 его курс к доллару США составлял 2,4 долл. (официальное золотое содержание равнялось 2,13281
г). С июня 1972 валютный паритет Ф. с. и относительно узкие рамки колебаний его курса официально не поддерживаются (введён «плавающий курс»). В июне 1977 курс Ф. с. к доллару США составил 1,72 долл. По курсу Госбанка СССР (июнь 1977) 1 Ф. с. = 1 руб. 28 коп.
Е. Д. Золотаренко.
Фуншал
Фунша'л(Funchal), главный город и порт о. Мадейра в Португалии, административный центр округа Фуншал. 38,3 тыс. жителей (1970). Виноделие, сахарная промышленность. Зимний курорт и центр туризма.
Фур
Фур,конджара, язык народности
(фур) в области Дарфур на З. Республики Судан. Число говорящих на Ф. около 350 тыс. чел. (1973, оценка). Предположительно относится к
. Небогатый консонантизм. Гласные различаются по 4 подъёмам. Морфология во многом флективная. Грамматические значения выражаются префиксами, суффиксами, а в глаголе — также внутренней флексией: und-

— «я собирал», b-ut- — «он собирал». Много типов спряжения и образования времён у глагола, образования множеств. числа у имени. Падежи имени оформляются агглютинативными суффиксами.
Лит.:Zyhlarz Е., Das Verbum im Kondjara, «Anthropos», 1926, Bd 21: Tucker A. N., Bryan M. A., Linguistic analyses. The Non-Bantu languages of North-Eastern Africa, L. — N. Y. — Cape Town, 1966; Greenberg J. H., The languages of Africa, 2 ed.. The Hague, 1966.
Фураж
Фура'ж(франц. fourrage), корма, заготавливаемые для с.-х. животных: зерно злаковых и бобовых культур (см.
), а также сено, солома, мякина и др. грубые корма.
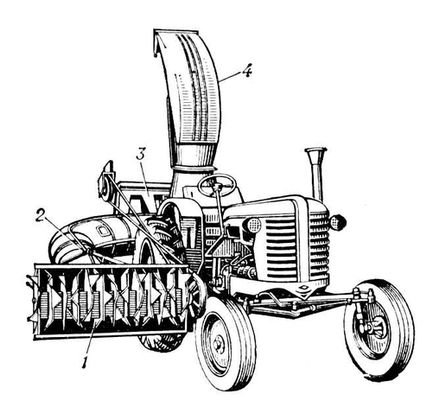
Фуражир навесной
Фуражи'р навесно'й,машина для измельчения и погрузки в транспортные средства соломы из скирд и силоса из наземных хранилищ. Ф. н. (
рис
.) агрегатируют с трактором класса 1,4
тс. Рабочие органы его приводятся в действие от вала отбора мощности трактора. Может забирать солому из скирд высотой до 5
м. Ширина захвата (длина барабана) 1200
мм. Производительность на измельчении соломы 6,5
т/ч, силоса 5,9
м/ч.
Агрегат из трактора и навесного фуражира: 1 — измельчающий барабан; 2 — конфузор, отсасывающий измельченную солому (силос) к эксгаустеру; 3 — рама машины; 4 — эксгаустер с дефлектором и направляющим козырьком, сбрасывающий корма в тракторную тележку.
Фуражировка
Фуражиро'вка,устаревший термин, означавший добывание и сбор в военное время выделенными от войск командами продовольствия и фуража (с полей и в населённых пунктах), а также доставка отопительных средств и строительных материалов для строительства дорог, мостов и укреплений.
Фуражный фонд
Фура'жный фонд,запас грубых, сочных и концентрированных кормов для общественного животноводства. Размер Ф. ф. устанавливают ежегодно в соответствии с нормами кормления с.-х. животных и их поголовьем (с учётом прироста и предполагаемой покупки скота). В дополнение к основному Ф. ф. из собранного урожая выделяют страховой фонд кормов.
Фуран
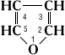
Фура'н,фурфуран, гетероциклическое соединение; бесцветная жидкость с запахом хлороформа,
t
kип31,33°C. Ф. — родоначальник большой группы органических соединений, многие из которых имеют практическое значение, например
,
, a-метилфуран (сильван).
Получают Ф. главным образом из фурфурола. Ф. — промежуточный продукт в синтезе тетрагидрофурана, используется также для получения
(реакцией с NH
3в присутствии A
2O
3). См. также
.
Фурановые смолы
Фура'новые смо'лы,олигомерные продукты, получаемые из соединений, содержащих фурановый цикл, способные при нагревании или в присутствии катализаторов превращаться в трёхмерные (сшитые) полимеры. Наиболее важные смолы получают из фурилового спирта, продуктов взаимодействия его с фурфуролом (фурфурилфурфураля) и фурфурола с ацетоном. Последние в щелочной среде при молярном соотношении 1: 1 образуют мономер ФА, представляющий собой главным образом смесь моно- (50—65%) и дифурфурилиденацетона (40—25%). Ф. с. образуются, как правило, при изготовлении из указанных продуктов композиционных материалов. Все смолы легко отверждаются при нагревании; процесс ускоряется в присутствии кислотных катализаторов, особенно ароматических сульфокислот и минеральных кислот (см.
).
Продукты отверждения отличаются высокими тепло-, кислото- и щёлочестойкостью, высоким коксовым числом (85—90%). Мономер ФА применяют как связующее в производстве
и полимерных замазок, которые в отличие от бетона содержат в качестве наполнителя мелкодисперсные порошки (песок, андезитовая мука в сочетании с углеграфитовым порошком). Замазки обладают более высокими механической прочностью, пластичностью, коррозионной стойкостью, меньшей хрупкостью, чем полимербетон; их применяют для защиты бетонных строительных конструкций в химических цехах, для футеровки химических аппаратов, особенно аппаратуры целлюлозно-бумажных производств. Полимеры фурилового спирта используют как связующее в производстве стеклопластиков, отличающихся очень высокой щёлоче- и теплостойкостью; фурфурилфурфуралевая смола, содержащая бензолсульфокислоту в качестве отвердителя, — связующее для стеклопластиков холодного отверждения. Ф. с. используются также как связующие в пресс-композициях с асбестовым волокном и графитом. См.
,
,
.
Г. М. Цейтлин.
Фуранозы
Фурано'зы,циклические формы
, содержащих пятичленный фурановый цикл. В отличие от шестичленной (пиранозной) формы, Ф. менее устойчивы и существуют для большинства моносахаридов только в водных растворах, притом в количествах, значительно меньших, чем пиранозы. Склонность к образованию фуранозного цикла явно выражена, например, у
, которая в виде Ф. входит также в состав многих олиго- и полисахаридов (например,
); большинство же моносахаридов в
, олиго- и полисахаридах имеют пиранозную форму. Гликозиды, в которых сахарная часть представлена Ф., называются фуранозидами.
Фурастье Жан
Фурастье'(Fourastiй) Жан (р.

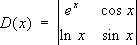 ,
,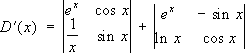 .
.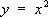 ,
,
 и т. п. К вычислительным (или аналитическим) операциям, кроме четырёх действий арифметики, принято относить также операцию перехода к пределу (т. е. нахождение по заданной последовательности чисел
a
1,
a
2,
a
3,... её
lim
a
n, если он существует), хотя никаких общих способов производства этой операции нет. В 1905 А.
предложил общее определение аналитически изобразимой Ф. как Ф., значения которой получаются из значений
xи постоянных величин при помощи арифметических действий и предельных переходов. Все т. н. элементарные Ф. sin
x, cos
x,
a
x,
и т. п. К вычислительным (или аналитическим) операциям, кроме четырёх действий арифметики, принято относить также операцию перехода к пределу (т. е. нахождение по заданной последовательности чисел
a
1,
a
2,
a
3,... её
lim
a
n, если он существует), хотя никаких общих способов производства этой операции нет. В 1905 А.
предложил общее определение аналитически изобразимой Ф. как Ф., значения которой получаются из значений
xи постоянных величин при помощи арифметических действий и предельных переходов. Все т. н. элементарные Ф. sin
x, cos
x,
a
x,
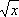 , log
x, arctg
xи т. п. аналитически изобразимы. Например, cos
xпредставляется формулой:
, log
x, arctg
xи т. п. аналитически изобразимы. Например, cos
xпредставляется формулой: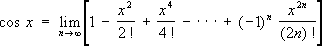 .
.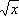 в алгебре как число, квадрат которого равен
x. Возможность задания этих Ф. при помощи аналитических формул устанавливается лишь при более углублённом их изучении. Упомянем ещё о т. н. функции Дирихле y(
x), равной 1, если
x— число рациональное, и 0, если
x— число иррациональное. Впервые эта Ф. была введена этим «бесформульным» способом, но впоследствии для неё была найдена и аналитическая формула:
в алгебре как число, квадрат которого равен
x. Возможность задания этих Ф. при помощи аналитических формул устанавливается лишь при более углублённом их изучении. Упомянем ещё о т. н. функции Дирихле y(
x), равной 1, если
x— число рациональное, и 0, если
x— число иррациональное. Впервые эта Ф. была введена этим «бесформульным» способом, но впоследствии для неё была найдена и аналитическая формула: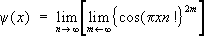 .
.
 — «я собирал», b-ut- — «он собирал». Много типов спряжения и образования времён у глагола, образования множеств. числа у имени. Падежи имени оформляются агглютинативными суффиксами.
— «я собирал», b-ut- — «он собирал». Много типов спряжения и образования времён у глагола, образования множеств. числа у имени. Падежи имени оформляются агглютинативными суффиксами.