 |
|
Популярные авторы:: Андерсон Пол Уильям :: Говард Роберт Ирвин :: Эллисон Харлан :: Лавкрафт Говард Филлипс :: Ломер Кит :: Желязны Роджер :: Дойл Артур Конан :: Гилберт Честертон :: БСЭ :: Шукшин Василий Макарович Популярные книги:: Справочник по реестру Windows XP :: Бурый волк :: Последний коммунист :: Дунайский лоцман :: Птичка певчая :: Шотландский лев :: Тень в зеркале :: Снежная страна :: Злой гений Нью-Йорка [Дело Епископа] :: Лопатка |
Большая Советская Энциклопедия (ЛИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЛИ) - Чтение (стр. 22)
здесь a ijи b i( i, j= 1, 2, ..., n) - произвольные числовые коэффициенты; числа b 1, b 2, ..., b nназывают обычно свободными членами. Если определитель D= ½a ij½ системы (2), составленный из коэффициентов a ijпри неизвестных, отличен от нуля, то решение получается следующим образом: k-e ( k= 1, 2, ..., n) неизвестное x kравно дроби, в знаменателе которой стоит определитель D, а в числителе - определитель, полученный из Dзаменой в нём столбца из коэффициентов при отыскиваемом неизвестном ( к-го столбца) столбцом свободных членов b 1, b 2, ..., b n. Если D= 0, то система (2) либо не имеет ни одного решения, либо имеет бесконечное множество решений. Если все b i= 0 (систему Л. у. называют в этом случае однородной), то при D¹ 0 решение системы (2) будет нулевым (т. е. все x k= 0). В практике часто, однако, встречаются однородные системы Л. у. с числом уравнений на 1 меньше числа неизвестных, т. е. системы вида:
Решение такой системы неоднозначно; из неё, как правило, можно найти только отношение неизвестных: x 1: x 2: ... : x n= D 1: D 2: ... : D n, где D n- умноженный на ( - 1) kопределитель, полученный из матрицы коэффициентов a ijсистемы (3) вычёркиванием какого-то столбца (это правило применимо только тогда, когда хотя бы один из определителей D iотличен от 0). Впервые решение систем (2) было получено Г. Крамером в 1750; правило для нахождения решения этих систем носит до сих пор название правила Крамера. Построение полной теории систем Л. у. было закончено только спустя 100 лет Л. Кронекером. Общая система mЛ. у. с nнеизвестными имеет вид:
Вопрос о совместности системы Л. у. (4), т. е. вопрос о существовании решения, решается сравнением рангов матриц
и
Если ранги совпадают, то система совместна; если ранг матрицы В больше ранга матрицы Л, то система несовместна (теорема Кронекера - Капелли). В случае совместности системы, её решения можно найти следующим образом. Найдя в матрице Аотличный от нуля минор наибольшего порядка г, отбрасывают m - rуравнений, коэффициенты которых не вошли в этот минор (отбрасываемые уравнения будут следствиями оставшихся, и поэтому их можно не рассматривать); в оставшихся уравнениях переносят направо те неизвестные, коэффициенты которых не вошли в выбранный минор (свободные неизвестные). Придав свободным неизвестным любые числовые значения, получают систему из rуравнений с rнеизвестными, которую можно решить по правилу Крамера. Найденные значения rнеизвестных вместе со значениями свободных неизвестных дадут некоторое частное (т. е. одно из многих возможных) решение системы (4). Можно, не давая свободным неизвестным конкретных значений, непосредственно выразить через них остальные неизвестные. Так получается общее решение, т. е. решение, в котором неизвестные выражены через параметры; давая этим параметрам произвольные значения, можно получить все частные решения системы. Однородные системы Л. у. можно решать таким же способом. Решения их обладают тем свойством, что сумма, разность и вообще любая линейная комбинация решений (рассматриваемых как n-мерные векторы) также будет решением системы. Другими словами: совокупность всех решений однородной системы Л. у. образует линейное подпространство n-мерного векторного пространства. Систему решений, которые сами линейно независимы и позволяют выразить любое другое решение в виде их линейной комбинации (т. е. базис линейного подпространства), называют фундаментальной системой решений однородной системы Л. у. Между решениями системы Л. у. (4) и соответствующей однородной системы Л. у. (т. е. уравнений с теми же коэффициентами при неизвестных, но со свободными членами, равными нулю) существует простая связь: общее решение неоднородной системы получается из общего решения однородной системы прибавлением к нему какого-либо частного решения неоднородной системы Л. у. Большой наглядности изложения в теории Л. у. можно добиться, используя геометрический язык. Привлекая при этом к рассмотрению линейные операторы в векторных пространствах (рассматривая уравнения вида Ax = b, А- линейный оператор, хи b- векторы), легко установить связь рассматриваемых алгебраических Л. у. с Л. у. в бесконечномерных пространствах (системы Л. у. с бесконечным числом неизвестных), в частности с Л. у. в функциональных пространствах, например линейные дифференциальные уравнения,линейные интегральные уравнения (см. Интегральные уравнения ) и др. Применение правила Крамера при практическом решении большого числа Л. у. может встретить значительные трудности, т. к. нахождение определителей высокого порядка связано со слишком большими вычислениями. Были поэтому разработаны различные методы численного (приближённого) решения систем Л. у. (см. Численное решение уравнений ) .
Лит.:Энциклопедия элементарной математики, под ред. П. С. Александрова [и др.], кн. 2, М. - Л., 1951; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М. - Л., 1963. Линейно-ленточной керамики культура Лине'йно-ле'нточной кера'мики культу'ра, археологическая культура эпохи раннего неолита (конец 5 - начало 4-го тыс. до н. э.), распространённая в Средней Европе. Является частью дунайских культур.Характеризуется единообразной керамикой сферических и полусферических форм, украшенной орнаментом из лент, состоящих из 2-3 углублённых линий (S-образные спирали, меандры). Линии иногда пересечены ямками («нотная керамика»). Из орудий характерны колодкообразные топоры. Известны крупные поселения этой культуры: Кёльн-Линденталь,Билани (Чехия), Флорешты (Молдавская ССР), состоящие из больших столбовых домов и землянок. Население занималось земледелием (пшеница, ячмень) и скотоводством (крупный и мелкий рогатый скот, свиньи). Лит.:Пассек Т. С., Черныш Е. К., Памятники культуры линейно-ленточной керамики на территории СССР, М., 1963; Hoffman Е., Die Kultur der Bandkerarnik in Sachsen, Tl 1 - Die Kerarnik, B., 1963. В. С. Титов. Линейные войска Лине'йные войска', 1) в 18-19 вв. в армиях различных государств Л. в. называли тяжёлую (линейную) пехоту, действовавшую в сомкнутом строю и наносившую главный удар, в отличие от лёгкой пехоты, которая действовала в рассыпном строю и выполняла вспомогательные задачи. Линейной иногда называлась также тяжёлая кавалерия. 2) Войска в русской армии, охранявшие главным образом пограничные укрепленные линии.Л. в. появились в 1804. К 1856 было 84 линейных батальона: 18 Грузинских, 16 Черноморских, 13 Кавказских, 12 Финляндских, 10 Оренбургских и 15 Сибирских. Все они (кроме Черноморских) сводились в пехотные бригады (по 5-7 батальонов), а Финляндские, Оренбургские и Сибирские, кроме того, и в пехотные дивизии. В 1858 Грузинские и Черноморские батальоны были переименованы в Кавказские, а в 1867 Оренбургские и часть Сибирских - в Туркестанские. К началу 20 в. все линейные войска были переформированы в стрелковые и резервные. В 1832-60 существовало Кавказское линейное казачье войско. Линейные дифференциальные уравнения Лине'йные дифференциа'льные уравне'ния, дифференциальные уравнения вида y ( n) + p 1( x) у ( n-1) + ... + p n( x) y = f( x) ,(1) где у = y( x) - искомая функция, y ( n) , у ( n-1) ,..., y'- её производные, a p 1( x) , p 2( x) ,..., p n( x) (коэффициенты) и f( x) (свободный член) - заданные функции (см. Дифференциальные уравнения ) .В уравнение (1) искомая функция у и её производные входят в 1-й степени, т. е. линейно, поэтому оно называется линейным. Если f( x) є 0, то уравнение (1) называется однородным, в противном случае - неоднородным. Общее решение y 0= y 0( x) однородного Л. д. у. при условии непрерывности его коэффициентов p k( x) выражается формулой: y 0= C 1y 1( x) + С 2у 2( х) + ... + C ny n( x) , где C 1, C 2,..., C n- произвольные постоянные и y 1( x) , у 2( х) ,..., y n( x) - линейно независимые (см. Линейная зависимость ) частные решения, образующие т. н. фундаментальную систему решений. Критерием линейной независимости решений служит неравенство нулю (хотя бы в одной точке) определителя Вроньского ( вронскиана ) :
Общее решение у = у( х) неоднородного Л. д. у. (1) имеет вид: y = y 0+Y, где y 0= y 0( x) - общее решение соответствующего однородного Л. д. у. и Y = Y( x) - частное решение данного неоднородного Л. д. у. Функция Y( x) может быть найдена по формуле:
где y k( x) - решения, составляющие фундаментальную систему решений однородного Л. д. у., и W k( x) - алгебраическое дополнение элемента y k ( n-1)( x) в определителе (2) Вроньского W( x). Если коэффициенты уравнения (1) постоянны: p k( x) = a k( k= 1, 2, ..., n), то общее решение однородного уравнения выражается формулой:
где a
k± ib
k(
k= 1, 2, ...,
m;
l n+ a 1l n-1+ ... +a n= 0, n k- кратности этих корней и C ks, D ks- произвольные постоянные. Пример. Для Л. д. у. y’’’ + у= 0 характеристическое уравнение имеет вид: l 3+ 1 = 0. Его корнями являются числа: l
1= -1; l
2=
Следовательно, общее решение этого уравнения таково:
Системы Л. д. у. имеют вид:
( j= 1, 2, ..., n). Общее решение однородной системы Л. д. у. [получаемой из системы (3), если все f j( x) є 0] даётся формулами:
( j= 1, 2, ..., n) где y j1, y j2, ..., y jn- линейно независимые частные решения однородной системы (т. е. такие, что определитель ½ y jk( x)½ ¹ 0 хотя бы в одной точке). В случае постоянных коэффициентов p jk( x) = a jkчастные решения однородной системы следует искать в виде:
( j= 1, 2, ..., n), где A js- неопределённые коэффициенты, a l k- корни характеристического уравнения
и m k- кратность этих корней. Полный анализ всех возможных здесь случаев проводится с помощью теории элементарных делителей [см. Нормальная (жорданова) форма матриц ] . Для решения Л. д. у. и систем Л. д. у. с постоянными коэффициентами применяются также методы операционного исчисления. Лит.:Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Смирнов В. И., Курс высшей математики, т. 2, 20 изд., М., 1967; т. 3, ч. 2, 8 изд., М., 1969; Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970. Линейные системы Лине'йные систе'мы, колебательные системы, свойства которых не изменяются при изменении их состояния, т. е. параметры Л. с., характеризующие её свойства (упругость, масса и коэффициент трения механической системы; ёмкость, индуктивность и активное сопротивление электрической системы), не зависят от величин, характеризующих состояние системы (от смещений и скоростей в случае механической системы, напряжений и токов в случае электрической системы). Параметры реальных систем всегда в той или иной степени зависят от их состояния, например коэффициент упругости пружины зависит от величины деформации (отклонения от закона Гука при больших деформациях), активное сопротивление проводника зависит от его температуры, которая, в свою очередь, зависит от силы протекающего по проводнику тока и т. д. Поэтому реальные системы можно рассматривать как Л. с. только в некоторых ограниченных пределах изменений их состояния, при которых допустимо пренебречь изменениями их параметров. Для очень большого числа реальных систем эти пределы оказываются весьма широкими, поэтому большинство задач можно решать, рассматривая реальные системы как Л. с. Примерами Л. с. могут служить: маятник (при малых амплитудах колебания), электрический колебательный контур, мостовая измерительная схема, системы автоматического управления и регулирования и др. В тех случаях, когда в пределах возможных изменений состояний реальной системы уже сказываются изменения её параметров, приходится учитывать нелинейность системы (см. Нелинейные системы ) . Л. с. обладают свойствами, существенно упрощающими анализ происходящих в них процессов. Процессы в Л. с. описываются линейными дифференциальными уравнениями (откуда и произошло их название). Причём, в различных по физической природе Л. с. процессы описываются одинаковыми по структуре уравнениями. На этом основано физ. и, в частности, электрическое моделирование Л. с., а также моделирование на ЦВМ. Л. с. играют большую роль в физике и технике, т. к. без искажения формы воспроизводят внешние воздействия, имеющие характер гармонических колебаний,и, во-вторых, в Л. с. справедлив суперпозиции принцип. Линейные ускорители Лине'йные ускори'телизаряженных частиц, ускорители, в которых траектории частиц близки к прямой линии; см. Ускорители заряженных частиц. Линейный двигатель Лине'йный дви'гатель, электродвигатель, у которого один из элементов магнитной системы разомкнут и имеет развёрнутую обмотку, создающую бегущее магнитное поле, а другой выполнен в виде направляющей, обеспечивающей линейное перемещение подвижной части двигателя. Л. д. постоянного тока состоит из якоря с расположенной на нём обмоткой, служащей одновременно коллектором (направляющий элемент), и разомкнутого магнитопровода с обмотками возбуждения (подвижная часть), расположенными так, что векторы сил, возникающих под полюсами магнитопровода, имеют одинаковое направление. Отличается простотой регулирования скорости перемещения подвижной части. Л. д. переменного тока могут быть асинхронными и синхронными. Якорь асинхронного Л. д. в виде бруска обычно прямоугольного сечения без обмоток закрепляется вдоль пути перемещения подвижной части двигателя, имеющей магнитопровод с развёрнутыми многофазными обмотками, питаемыми от источника переменного тока. Вследствие взаимодействия магнитного поля в магнитопроводе подвижной части с полем якоря возникают силы, которые заставляют перемещаться с ускорением подвижную часть Л. д. относительно неподвижного якоря до тех пор, пока скорости перемещения двигателя и бегущего магнитного поля не уравняются. Наиболее перспективно применение асинхронных Л. д. в тяговых электроприводах транспортных машин в сочетании с магнитными и воздушными подушками, что даёт возможность повысить скорость движения поездов до 450-500 км/ч.Синхронные Л. д. практически не изготовляются. Основное достоинство Л. д. - способность создавать большие усилия и, как следствие этого, возможность развития значительных ускорений, что особенно важно для транспортных средств, а также отсутствие редуктора в конструкции двигателя. Лит.:Knuth I., Electrische Maschinen mit geradliniger Bewegung und ihre technische Anwendung, «Electro-Praktiker», 1969, № 1. Ю. М. Иньков. Линейный корабль Лине'йный кора'бль, линкор, 1) в парусном военном флоте 17-1-й половине 19 вв. крупный по размерам трёхмачтовый боевой корабль с 2-3 артиллерийскими палубами (деками); имел от 60 до 135 орудий, устанавливавшихся по бортам в линию и до 800 человек экипажа. Вёл бой, находясь в кильватерной колонне (линии баталии), отчего и получил своё название, перешедшее по традиции к кораблям парового флота. 2) В паровом броненосном флоте один из основных классов самых крупных по размерам артиллерийских надводных кораблей, предназначенных для уничтожения в морском бою кораблей всех классов, а также нанесения мощных артиллерийских ударов по береговым объектам. Л. к. появились во многих флотах мира после русско-японской войны 1904-05 взамен броненосцев.Сначала назывались дредноутами. В России название класса Л. к. установлено в 1907. Л. к. применялись в 1-й мировой войне 1914-18. К началу 2-й мировой войны 1939-45 Л. к. имели стандартное водоизмещение от 20 до 64 тыс. т,вооружение - до 12 башенных орудий главного калибра (от 280 до 460 мм) ,до 20 орудий противоминной, зенитной или универсальной артиллерии калибра 100-127 мм,до 80-140 зенитных малокалиберных автоматических пушек и крупнокалиберных пулемётов. Скорость хода Л. к. - 20-35 узлов (37-64,8 км/ч) ,экипаж военного времени - 1500-2800 человек. Бортовая броня достигала 440 мм,вес всей брони составлял до 40% общего веса корабля. На борту Л. к. имелись 1-3 самолёта и катапульта для их взлёта. В ходе войны в связи с возрастанием роли морской, особенно авианосной авиации,а также подводных сил флота и гибелью многих Л. к. от ударов авиации и подводных лодок они утратили значение; после войны во всех флотах почти все Л. к. сданы на слом. Б. Ф. Балев. 
Линейный корабль «Айова» (США). 1943. Линейный крейсер Лине'йный кре'йсер, подкласс крейсеров с мощным артиллерийским вооружением, появившийся перед 1-й мировой войной 1914-18. Было построено лишь несколько Л. к., имели водоизмещение от 20 до 42 тыс. т,вооружение - 6-9 башенных орудий калибра 280-380 мм,до 20 113- мморудий, скорость хода 29-30 узлов (53,7-55,5 км/ч) .Л. к. применялись в 1-й мировой войне, а три из оставшихся в ВМС Великобритании и во 2-й мировой войне 1939-45. После войны последний уцелевший Л. к. был сдан на слом. Линейный оператор Лине'йный опера'тор, обобщение понятия линейного преобразования на линейные пространства.Линейным оператором Fна линейном пространстве Еназывают функцию F( x), определённую для всех хО Е, значения которой суть элементы линейного пространства E 1, и обладающую свойством линейности: F(( x +( у) =( F( x) +( F( y) ,
где
хи
у- любые элементы из
Е, a и b - числа. Если пространства
Еи
E
1нормированы и величина
Важнейшими конкретными примерами Л. о. в функциональных пространствах являются дифференциальные Л. о.
и интегральные Л. о.
примером Л. о. функций многих переменных может служить Лапласа оператор.Теория Л. о. находит большое применение в различных вопросах математической физики и прикладной математики. См. также Функциональный анализ , Операторов теория, Спектральный анализ(математический), Собственные значения и собственные функции, Собственные векторы. Линейный функционал Лине'йный функциона'л, обобщение понятия линейной формы на линейные пространства.Линейным функционалом fна линейном нормированном пространстве Еназывают числовую функцию f( x), определённую для всех хиз Еи обладающую следующими свойствами: 1) f( x) линейна, т. е. f(( x +( у) =( f( x) +( f( y), где хи у- любые элементы из Е, a и b - числа; 2) f( x) непрерывна. Непрерывность
fравносильна требованию, чтобы
В пространстве
С[
a, b] функций a(t), непрерывных при
a(
t(
b, с нормой
f 2[(( t) ] =(( t 0) , a( t 0( b. В гильбертовом пространстве Н Л. ф. суть скалярные произведения ( l, х), где l- любой фиксированный элемент пространства Н; ими исчерпываются все Л. ф. этого пространства. Во многих задачах можно из общих соображений установить, что та или иная величина является Л. ф. Например, к Л. ф. приводит решение линейных дифференциальных уравнений с линейными краевыми условиями. Поэтому очень существенным является вопрос об общем аналитическом выражении Л. ф. в разных пространствах. Совокупность всех Л. ф. данного пространства
Епревращается в линейное нормированное пространство
С понятием Л. ф. связано понятие слабой сходимости. Последовательность { xn} элементов линейного нормированного пространства называют слабо сходящейся к элементу х, если
для любого Л. ф. f. См. также Функциональный анализ. Линейных знаков способ Лине'йных зна'ков спо'соб, один из картографических способов изображения.Л. з. с. изображаются линии местности (например, водоразделы, тектонические разломы, линии связи, политико-административные границы и др.), объекты линейного протяжения, не выражающиеся в масштабе карты (например, реки и дороги и др.), граничные полосы (например, береговая зона, зональные границы почв и растительности и др.). Линейчатая геометрия Лине'йчатая геоме'трия, раздел геометрии, в котором рассматриваются в качестве элементов пространства прямые линии. Как известно, прямая в пространстве определяется четырьмя постоянными - коэффициентами а, b, р, qв уравнениях х = az + р, у = bz + q. Следовательно, величины а, b, р, q можно рассматривать как координаты прямой. Если эти координаты являются функциями одного, двух или трёх параметров, то соответствующие совокупности прямых образуют линейчатые поверхности и т. н. конгруэнции и комплексы прямых. Эти геометрические образы и являются объектом изучения Л. г. Примером линейчатой поверхности может служить однополостный гиперболоид, примером конгруэнции - совокупность общих касательных к двум каким-либо поверхностям, примером комплекса прямых - совокупность касательных к одной какой-либо поверхности. Для изучения линейчатых поверхностей, конгруэнций и комплексов прямых с единой точки зрения в Л. г. вводятся так называемые линейные однородные координаты прямой. Пусть заданы две точки M 1( x 1, y 1, z 1) и M 2( x 2, y 2, z 2) ,тогда линейными однородными координатами прямой, проходящей через эти точки, называют шесть чисел, пропорциональных (или равных) числам: x 1= x 1- x 2, x 2= y 1- y 2, x 3= z 1- z 2, x 4= y 1z 2- y 2z 1, x 5= x 2z 1- x 1z 2, x 6= x 1y 2- x 2y 1. Числа x
1, x
2, x
3являются компонентами вектора
x 1x 4+ x 2x 5+ x 3x 6= 0. (1) Таким образом, каждой прямой соответствуют шесть определяемых с точностью до постоянного множителя чисел x i, удовлетворяющих соотношению (1), и обратно, числа x i(не все равные нулю), связанные условием (1), определяют единственным образом некоторую прямую (как её координаты в указанном выше смысле). Одно однородное линейное уравнение
определяет линейный комплекс - совокупность прямых, заполняющих пространство так, что через каждую точку пространства проходит пучок прямых, лежащих в одной плоскости. Таким образом, каждой точке («полюсу») пространства можно поставить в соответствие плоскость («полярную плоскость»), содержащую все прямые комплекса, проходящую через эту точку. Это соответствие называют нулевой системой; оно аналогично соответствию полюсов и полярных плоскостей поверхности 2-го порядка. Если полярные плоскости всех точек пространства проходят через одну прямую (ось), то комплекс состоит из всех прямых, пересекающих ось; его называют специальным линейным комплексом. В этом случае коэффициенты уравнения (2) удовлетворяют условию a 1a 4+ a 2a 5+ a 3a 6= 0. Система двух однородных линейных уравнений вида (2) определяет линейную конгруэнцию - совокупность прямых, пересекающих две данные прямые (которые могут быть и мнимыми). Три однородных линейных уравнения определяют линейчатую поверхность, являющуюся в этом случае либо однополостным гиперболоидом, либо гиперболическим параболоидом. Линейные однородные координаты прямой были введены Ю. Плюккером в 1846. Он же подробно изучил теорию линейного комплекса. В дальнейшем Л. г. разрабатывалась в работах Ф. Клейна и русского математика А. П. Котельникова. Дифференциальная геометрия конгруэнций, начатая Э. Куммером в 1860, получила большое развитие в трудах итальянских математиков Л. Бианки, Г. Санниа и французского математика А. Рибокура. На основе созданного в 1895 Котельниковым «винтового» исчисления советским математиком Д. Н. Зейлигером развита теория линейчатых поверхностей и конгруэнций. Проективная теория конгруэнций построена в 1927 советским математиком С. П. Финиковым. Лит.:Зейлигер Д. Н., Комплексная линейчатая геометрия. Поверхности и конгруэнции, Л. - М., 1934; Фиников С. П., Теория поверхностей, М. - Л., 1934; его же, Проективно-дифференциальная геометрия, М. - Л.,1937; его же, Теория конгруэнций, М. - Л., 1950; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1-2, М. - Л., 1947-48; Клейн Ф., Высшая геометрия, пер. с нем., М. - Л., 1939; Zindler К., Liniengeometrie, Bd 1-2, Lpz., 1902-06. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59 |
|||||||
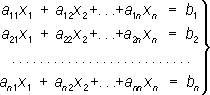 (2)
(2)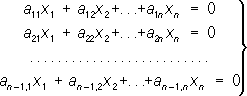 (3)
(3)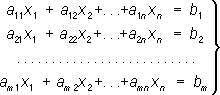 (4)
(4)

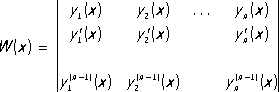 (2)
(2)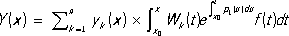 ,
,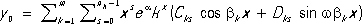 ,
,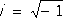 ) - корни т. н. характеристического уравнения:
) - корни т. н. характеристического уравнения: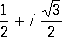 и l
3=
и l
3=
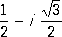
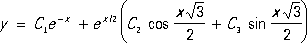 .
.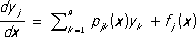 (3)
(3)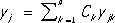
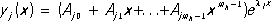
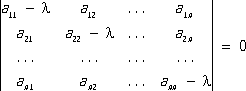
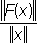 ограничена, то Л. о. F называют ограниченным, а
ограничена, то Л. о. F называют ограниченным, а
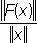 его нормой.
его нормой.
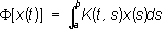
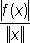 было ограничено в
Е; выражение
было ограничено в
Е; выражение
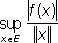 называют нормой
fи обозначают
называют нормой
fи обозначают
 .
.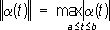 Л. ф. являются, например, выражения:
Л. ф. являются, например, выражения: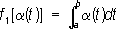 ,
,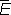 , если определить естественным образом сложение Л. ф. и умножение их на числа. Пространство
, если определить естественным образом сложение Л. ф. и умножение их на числа. Пространство
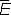 называют сопряжённым к
называют сопряжённым к
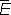 ; это пространство играет большую роль при изучении
Е.
; это пространство играет большую роль при изучении
Е.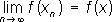
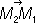 , а x
4, x
5, x
6- компоненты момента этого вектора относительно начала координат. Легко проверить, что числа x
iудовлетворяют соотношению
, а x
4, x
5, x
6- компоненты момента этого вектора относительно начала координат. Легко проверить, что числа x
iудовлетворяют соотношению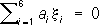 (2)
(2)