 |
|
Популярные авторы:: Эллисон Харлан :: Желязны Роджер :: Говард Роберт Ирвин :: Ломер Кит :: Лавкрафт Говард Филлипс :: Шукшин Василий Макарович :: Родари Джанни :: Ламур Луис :: Дойл Артур Конан :: Силверберг Роберт Популярные книги:: Справочник по реестру Windows XP :: Бурый волк :: Снежная страна :: Лопатка :: Последний коммунист :: Дунайский лоцман :: Птичка певчая :: Вирусы мозга :: Шотландский лев :: Иди и смотри |
Большая Советская Энциклопедия (СИ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (СИ) - Чтение (стр. 35)
 Н. Ф. Степанов. Симметрия кристаллов Симме'трия криста'ллов,свойство кристаллов совмещаться с собой в различных положениях путём поворотов, отражений, параллельных переносов либо части или комбинации этих операций. Симметрия внешней формы (огранки) кристалла определяется симметрией его атомного строения, которая обусловливает также и симметрию физических свойств кристалла.  На рис. 1 , а изображен кристалл кварца . Внешняя его форма такова, что поворотом на 120° вокруг оси 3 он может быть совмещен сам с собой (совместимое равенство). Кристалл метасиликата натрия ( рис. 1 , б) преобразуется в себя отражением в плоскости симметрии m(зеркальное равенство). Т. о., симметрия означает возможность преобразования объекта совмещающего его с собой. Если F( x 1, x 2, x 3) - функция, описывающая объект, например форму кристалла в трёхмерном пространстве или какое-либо его свойство, а операция g[ x 1, x 2, x 3] осуществляет преобразование координат всех точек объекта, то gявляется операцией или преобразованием симметрии, а F- симметричным объектом, если выполняются условия:
g[
x
1,.
x
2,
x
3]
=
F( x 1, x 2, x 3) = F( x 2, x 2, x 3).В В В В (1, Р±) В Р’ наиболее общей формулировке симметрия - неизменность (инвариантность) объектов РїСЂРё некоторых преобразованиях описывающих РёС… переменных. Кристаллы - объекты РІ трёхмерном пространстве, поэтому классическая теория РЎ. Рє. - теория симметрических преобразований РІ себя трёхмерного пространства СЃ учётом того, что внутренняя атомная структура кристаллов - трёхмерно-периодическая, С‚. Рµ. описывается как кристаллическая решётка . РџСЂРё преобразованиях симметрии пространство РЅРµ деформируется, Р° преобразуется как жёсткое целое (ортогональное, или изометрическое, преобразование). После преобразования симметрии части объекта, находившиеся РІ РѕРґРЅРѕРј месте, совпадают СЃ частями, находящимися РІ РґСЂ. месте. Рто означает, что РІ симметричном объекте есть равные части (совместимые или зеркальные). В РЎ. Рє. проявляется РЅРµ только РІ РёС… структуре Рё свойствах РІ реальном трёхмерном пространстве, РЅРѕ также Рё РїСЂРё описании энергетического спектра электронов кристалла РІ импульсном пространстве (СЃРј. Твёрдое тело ), РїСЂРё анализе процессов дифракции рентгеновских лучей РІ кристаллах СЃ помощью пространства обратных длин Рё С‚. Рї.  Группа симметрии кристаллов.Кристаллу может быть присуща РЅРµ РѕРґРЅР°, Р° несколько операций симметрии. Так, кристалл кварца ( СЂРёСЃ. 1 , Р°) совмещается СЃ СЃРѕР±РѕР№ РЅСЃ только РїСЂРё повороте РЅР° 120В° РІРѕРєСЂСѓРі РѕСЃРё 3 (операция g 1), РЅРѕР№ РїСЂРё повороте РІРѕРєСЂСѓРі РѕСЃРё 3 РЅР° 240В° (операция g 2), Р° также РїСЂРё поворотах РЅР° 180В° РІРѕРєСЂСѓРі осей 2 x, 2 y, 2 w(операции g 3, g 4Рё g 5). Каждой операции симметрии может быть сопоставлен геометрический образ - элемент симметрии - прямая, плоскость или точка, относительно которой производится данная операция. Например, РѕСЃСЊ 3 или РѕСЃРё 2 x, 2 y, 2 wявляются РѕСЃСЏРјРё симметрии, плоскость m( СЂРёСЃ. 1 , Р±) - плоскостью зеркальной симметрии Рё С‚. Рї. Совокупность операций симметрии [ g 1,..., g n] данного кристалла образует РіСЂСѓРїРїСѓ симметрии GРІ смысле математической теории РіСЂСѓРїРї . Последовательное проведение РґРІСѓС… операций симметрии также является операцией симметрии. Всегда существует операция идентичности g 0, ничего РЅРµ изменяющая РІ кристалле, называется отождествлением, геометрически соответствующая неподвижности объекта или повороту его РЅР° 360В° РІРѕРєСЂСѓРі любой РѕСЃРё. Число операций, образующих РіСЂСѓРїРїСѓ G, называется РїРѕСЂСЏРґРєРѕРј РіСЂСѓРїРїС‹.  Группы симметрии классифицируют: РїРѕ числу nизмерений пространства, РІ которых РѕРЅРё определены; РїРѕ числу тизмерений пространства, РІ которых объект периодичен (РёС… соответственно обозначают G m n) Рё РїРѕ некоторым РґСЂСѓРіРёРј признакам. Для описания кристаллов используют различные РіСЂСѓРїРїС‹ симметрии, РёР· которых важнейшими являются пространственные РіСЂСѓРїРїС‹ симметрии G 3 3, описывающие атомную структуру кристаллов, Рё точечные РіСЂСѓРїРїС‹ симметрии G 0 3, описывающие РёС… внешнюю форму. Последние называются также кристаллографическими классами. В
Симметрия огранки кристаллов.Операциями точечной симметрии являются: повороты вокруг оси симметрии порядка
NРЅР° 360В°/
N(
СЂРёСЃ. 2
, а), отражение в плоскости симметрии (зеркальное отражение,
СЂРёСЃ. 2
, б), инверсия
 Точечные преобразования симметрии
g[
x
1,
x
2,
x
3] =
x' 1= а 11 х 1+ a 12 x 2+ a 13 x 3, x' 2= a 21 x 1+ a 22 x 2+ a 23 x 3,    (2) x' 3= a 31 x 1+ a 32 x 2+ a 33 x 3, т. е. матрицей коэффициента ( a ij). Например, при повороте вокруг хзна угол a = 360°/ Nматрица коэффициентов имеет вид:
а при отражении в плоскости x 1, x 2имеет вид:
Поскольку
Nможет быть любым, число групп
 Группы, содержащие лишь повороты, описывают кристаллы, состоящие только РёР· совместимо равных частей. Рти РіСЂСѓРїРїС‹ называются группами 1-РіРѕ СЂРѕРґР°. Группы, содержащие отражения, или инверсионные повороты, описывают кристаллы, РІ которых есть зеркально равные части (РЅРѕ РјРѕРіСѓС‚ быть Рё совместимо равные части). Рти РіСЂСѓРїРїС‹ называются группами 2-РіРѕ СЂРѕРґР°. Кристаллы, описываемые группами 1-РіРѕ СЂРѕРґР°, РјРѕРіСѓС‚ кристаллизоваться РІ РґРІСѓС… энантиоморфных формах, условно называемых «правой» Рё «левой», каждая РёР· РЅРёС… РЅРµ содержит элементов симметрии 2-РіРѕ СЂРѕРґР°, РЅРѕ РѕРЅРё зеркально равны РґСЂСѓРі РґСЂСѓРіСѓ (СЃРј. Рнантиоморфизм , Кварц ).  Точечные РіСЂСѓРїРїС‹ описывают симметрию РЅРµ только кристаллов, РЅРѕ любых конечных фигур. Р’ живой РїСЂРёСЂРѕРґРµ часто наблюдается запрещенная РІ кристаллографии симметрия СЃ РѕСЃСЏРјРё 5-РіРѕ, 7-РіРѕ РїРѕСЂСЏРґРєР° Рё выше. Например, для описания регулярной структуры сферических РІРёСЂСѓСЃРѕРІ ( СЂРёСЃ. 4 ), РІ оболочках которых соблюдаются кристаллографические принципы плотной укладки молекул, оказалась важной икосаэдрическая точечная РіСЂСѓРїРїР° 532.  Симметрия физических свойств. Предельные РіСЂСѓРїРїС‹.Р’ отношении макроскопических физических свойств (оптических, электрических, механических Рё РґСЂ.), кристаллы ведут себя как однородная анизотропная среда, С‚. Рµ. дискретность РёС… атомной структуры РЅРµ проявляется. Однородность означает, что свойства одинаковы РІ любой точке кристалла, однако РїСЂРё этом РјРЅРѕРіРёРµ свойства зависят РѕС‚ направления (СЃРј. Анизотропия ). Зависимость РѕС‚ направления можно представить РІ РІРёРґРµ функции Рё построить указательную поверхность данного свойства ( СЂРёСЃ. 5, СЃРј. также СЃС‚. Кристаллооптика ). Рта функция, которая может быть различной для разных физических свойств кристалла (векторной или тензорной) имеет определённую точечную симметрию, однозначно связанную СЃ РіСЂСѓРїРїРѕР№ симметрии огранения кристалла. РћРЅР° либо совпадает СЃ ней, либо выше её РїРѕ симметрии (принцип Неймана). В РњРЅРѕРіРёРµ РёР· свойств кристаллов, принадлежащих Рє определённым классам, описываются предельными точечными группами, содержащими РѕСЃРё симметрии бесконечного РїРѕСЂСЏРґРєР°, обозначаемые Тђ. Наличие РѕСЃРё Тђ означает, что объект совмещается СЃ СЃРѕР±РѕР№ РїСЂРё повороте РЅР° любой, РІ том числе бесконечно малый СѓРіРѕР». Таких РіСЂСѓРїРї 7, РѕРЅРё представлены РЅР° СЂРёСЃ. 6 образцовыми фигурами Рё соответствующими символами. Рў. Рѕ., всего имеется 32 + 7 = 39 точечных РіСЂСѓРїРї, описывающих симметрию свойств кристаллов. Зная РіСЂСѓРїРїСѓ РЎ. Рє., можно указать возможность наличия или отсутствия РІ нём некоторых физических свойств (СЃРј. Кристаллы , Кристаллофизика ). Обозначения Рё названия 32 РіСЂСѓРїРї точечной симметрии
 Пространственная симметрия атомной структуры кристаллов(кристаллической решётки) описывается пространственными группами симметрии
 Вследствие возможности комбинирования в решётке трансляций и операций точечной симметрии в группах G 3 3возникают операции и соответствующие им элементы симметрии с трансляционной компонентой - винтовые оси различных порядков и плоскости скользящего отражения ( рис. 2 , д).  Всего известно 230 пространственных (фёдоровских) групп симметрии
В
Симметрия слоев и цепей.Для описания плоских или вытянутых в одном направлении фрагментов структуры кристаллов могут быть использованы группы
 Обобщённая симметрия.В основе определения симметрии лежит понятие равенства ( 1 , б) при преобразовании ( 1 , а). Однако физически (и математически) объект может быть равен себе по одним признакам и не равен по другим. Например, распределение ядер и электронов в кристалле антиферромагнетика можно описать с помощью обычной пространственной симметрии, но если учесть распределение в нём магнитных моментов ( рис. 9 ), то «обычной», классической симметрии уже недостаточно. К подобного рода обобщениям симметрии относится антисимметрия и цветная симметрия. В антисимметрии в дополнение к трём пространственным переменным x 1, x 2, x 3вводится добавочная, 4-я переменная x 4= ± 1. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 В В В В
В (1,
a)
В В В В
В (1,
a)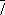 (симметрия относительно точки,
СЂРёСЃ. 2
, в), инверсионные повороты
(симметрия относительно точки,
СЂРёСЃ. 2
, в), инверсионные повороты
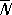  (комбинация поворота на 360°/
Nс одновременной инверсией,
СЂРёСЃ. 2
, г). Вместо инверсионных поворотов иногда рассматривают зеркальные повороты
 (комбинация поворота на 360°/
Nс одновременной инверсией,
СЂРёСЃ. 2
, г). Вместо инверсионных поворотов иногда рассматривают зеркальные повороты
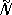 . Геометрически возможные сочетания этих операций определяют ту или иную точечную группу (
СЂРёСЃ. 3
), которые изображаются обычно в стереографической проекции. При преобразованиях точечной симметрии по крайней мере одна точка объекта остаётся неподвижной - преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции.
. Геометрически возможные сочетания этих операций определяют ту или иную точечную группу (
СЂРёСЃ. 3
), которые изображаются обычно в стереографической проекции. При преобразованиях точечной симметрии по крайней мере одна точка объекта остаётся неподвижной - преобразуется сама в себя. В ней пересекаются все элементы симметрии, и она является центром стереографической проекции.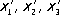  описываются линейными уравнениями:
 описываются линейными уравнениями: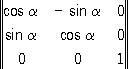 ,    (3)
,В В В В (3)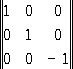 В В В В (3a)
    (3a)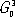  бесконечно. Однако в кристаллах ввиду наличия кристаллической решётки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го), которые обозначаются символами:
1,
2,
3,
4,
6, а также инверсионные оси:
 бесконечно. Однако в кристаллах ввиду наличия кристаллической решётки возможны только операции и соответственно оси симметрии до 6-го порядка (кроме 5-го), которые обозначаются символами:
1,
2,
3,
4,
6, а также инверсионные оси:
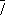  (она же центр симметрии),
 (она же центр симметрии),
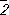 В =
m(она же плоскость симметрии),
В =
m(она же плоскость симметрии),
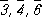 . Поэтому количество точечных кристаллографических РіСЂСѓРїРї, описывающих внешнюю форму кристаллов, ограничено. Рти 32 РіСЂСѓРїРїС‹ РЎ. Рє. приведены РІ таблице. Р’ международные обозначения точечных РіСЂСѓРїРї РІС…РѕРґСЏС‚ символы основных (порождающих) элементов симметрии, РёРј присущих. Рти РіСЂСѓРїРїС‹ объединяются РїРѕ симметрии формы элементарной ячейки (СЃ периодами
Р°,
b,
си углами a, b, g) в 7
сингоний кристаллографических
- триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Принадлежность кристалла к той или иной группе определяется гониометрически (см.
Гониометр
) или рентгенографически (см.
Рентгеновский структурный анализ
).
. Поэтому количество точечных кристаллографических РіСЂСѓРїРї, описывающих внешнюю форму кристаллов, ограничено. Рти 32 РіСЂСѓРїРїС‹ РЎ. Рє. приведены РІ таблице. Р’ международные обозначения точечных РіСЂСѓРїРї РІС…РѕРґСЏС‚ символы основных (порождающих) элементов симметрии, РёРј присущих. Рти РіСЂСѓРїРїС‹ объединяются РїРѕ симметрии формы элементарной ячейки (СЃ периодами
Р°,
b,
си углами a, b, g) в 7
сингоний кристаллографических
- триклинную, моноклинную, ромбическую, тетрагональную, тригональную, гексагональную и кубическую. Принадлежность кристалла к той или иной группе определяется гониометрически (см.
Гониометр
) или рентгенографически (см.
Рентгеновский структурный анализ
).
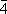
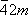
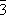
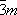
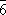
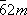
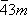
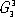 . Характерными для решётки операциями являются три некомпланарных переноса
Р°,
b,
с, называемых трансляциями, которые задают трёхмерную периодичность атомной структуры кристаллов. Сдвиг (перенос) структуры на векторы
a
1,
b
2,
c
3или любой вектор
t=
p
1a
1+
p
2b
2+
p
3c
3, РіРґРµ
p
1,
p
2,
p
3- любые целые положительные или отрицательные числа, совмещает структуру кристалла с собой, и следовательно, является операцией симметрии, удовлетворяющей условиям (
1
, а, б). Параллелепипед, построенный на векторах
Р°,
bРё
c, называется параллелепипедом повторяемости или элементарной ячейкой кристалла (
СЂРёСЃ. 7
, Р°, Р±). Р’ элементарной ячейке содержится некоторая минимальная РіСЂСѓРїРїРёСЂРѕРІРєР° атомов, «размножение» которой операциями симметрии, РІ том числе трансляциями, образует кристаллическую решётку. Рлементарная ячейка Рё размещение РІ ней атомов устанавливается методами
рентгеновского структурного анализа
,
электронографии
или
нейтронографии
.
. Характерными для решётки операциями являются три некомпланарных переноса
Р°,
b,
с, называемых трансляциями, которые задают трёхмерную периодичность атомной структуры кристаллов. Сдвиг (перенос) структуры на векторы
a
1,
b
2,
c
3или любой вектор
t=
p
1a
1+
p
2b
2+
p
3c
3, РіРґРµ
p
1,
p
2,
p
3- любые целые положительные или отрицательные числа, совмещает структуру кристалла с собой, и следовательно, является операцией симметрии, удовлетворяющей условиям (
1
, а, б). Параллелепипед, построенный на векторах
Р°,
bРё
c, называется параллелепипедом повторяемости или элементарной ячейкой кристалла (
СЂРёСЃ. 7
, Р°, Р±). Р’ элементарной ячейке содержится некоторая минимальная РіСЂСѓРїРїРёСЂРѕРІРєР° атомов, «размножение» которой операциями симметрии, РІ том числе трансляциями, образует кристаллическую решётку. Рлементарная ячейка Рё размещение РІ ней атомов устанавливается методами
рентгеновского структурного анализа
,
электронографии
или
нейтронографии
.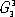 , и любой кристалл относится к одной из этих групп. Трансляционные компоненты элементов микросимметрии макроскопически не проявляются, например винтовая ось в огранке кристаллов проявляется как соответствующая по порядку простая поворотная ось. Поэтому каждая из 230 групп
, и любой кристалл относится к одной из этих групп. Трансляционные компоненты элементов микросимметрии макроскопически не проявляются, например винтовая ось в огранке кристаллов проявляется как соответствующая по порядку простая поворотная ось. Поэтому каждая из 230 групп
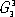  макроскопически сходственна с одной из 32 точечных групп. Например, точечной группе
mmmили
D
2hсходственны 28 пространственных групп. Совокупность переносов, присущих данной пространственной группе, есть её трансляционная подгруппа, или
Браве решётка
; таких решёток существует 14.
 макроскопически сходственна с одной из 32 точечных групп. Например, точечной группе
mmmили
D
2hсходственны 28 пространственных групп. Совокупность переносов, присущих данной пространственной группе, есть её трансляционная подгруппа, или
Браве решётка
; таких решёток существует 14.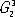  - двумерно периодические и
 - двумерно периодические и
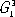 В - одномерно периодические РІ трёхмерном пространстве. Рти РіСЂСѓРїРїС‹ играют важную роль РІ изучении биологических структур Рё молекул. Например, РіСЂСѓРїРїС‹
В - одномерно периодические РІ трёхмерном пространстве. Рти РіСЂСѓРїРїС‹ играют важную роль РІ изучении биологических структур Рё молекул. Например, РіСЂСѓРїРїС‹
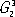  описывают строение биологических
мембран
, РіСЂСѓРїРїС‹
 описывают строение биологических
мембран
, РіСЂСѓРїРїС‹
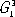  - цепных молекул (
СЂРёСЃ. 8
, а) палочкообразных
РІРёСЂСѓСЃРѕРІ
, трубчатых кристаллов глобулярных
белков
(
СЂРёСЃ. 8
, б), в которых молекулы уложены согласно спиральной (винтовой) симметрии, возможной в группах
 - цепных молекул (
СЂРёСЃ. 8
, а) палочкообразных
РІРёСЂСѓСЃРѕРІ
, трубчатых кристаллов глобулярных
белков
(
СЂРёСЃ. 8
, б), в которых молекулы уложены согласно спиральной (винтовой) симметрии, возможной в группах
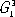 .
.