Вероятностная бумага

Вероя'тностная бума'ганормальная, специальным образом разграфленная бумага, построенная так, что график функции нормального распределения изображается на ней прямой линией. Это достигается изменением шкалы на вертикальной оси (см. рис. ). На свойстве «выпрямления» основан простой способ проверки гипотезы о принадлежности данной выборки к нормальной совокупности: если построенная на В. б. эмпирическая функция распределения хорошо приближается прямой линией, то можно с основанием полагать, что совокупность, из которой взята выборка, является приближённо нормальной. Достоинство этого метода состоит в том, что вывод о принадлежности к нормальной совокупности можно сделать без знания численных значений параметров гипотетического распределения.

  Лит.:Арлей Н., Бух К. P., Введение в теорию вероятностей и математическую статистику, пер. с англ., М., 1951; Dixon W. J., Massey F. J., Introduction to statistical analysis, N. Y. - Toronto - L., 1957.

  А. В. Прохоров.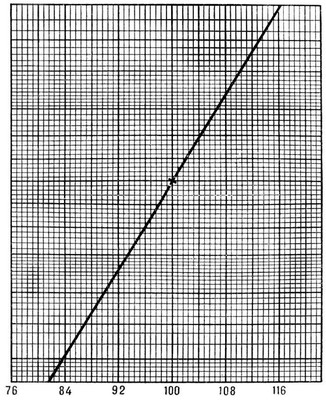

Образец вероятностной бумаги. Проведённая линия - график функции нормального распределения со средним 100 и стандартным отклонением 8.

Вероятностная логика

Вероя'тностная ло'гика,логическая система, в которой высказываниям (суждениям, утверждениям, предложениям), помимо истины и лжи, приписываются «промежуточные» истинностные значения, называемые вероятностями истинности высказываний, степенями их правдоподобия, степенями подтверждения и т.п. Поскольку понятие вероятности естественно соотносить некоторым событиям,а наступление или не наступление события есть факт, допускающий (хотя бы в принципе) эмпирическую проверку (в широком смысле - включая так называемый мысленный эксперимент, а также вывод из знания о наступлении или не наступлении др. событий), то В. л. представляет собой уточнение индуктивной логики.Взаимные переходы от языка высказываний к языку событий и обратно совершаются настолько естественно, что выглядят почти тривиальными: каждому событию сопоставляется высказывание о его наступлении, а высказыванию сопоставляется событие, состоящее в том, что оно оказалось истинным. Специфика В. л. (даже полностью формализованной в логико-математических терминах) состоит в принципиальной неустранимости неполной достоверности («относительной истинности») посылок и выводов, присущей всякому индуктивному познанию.

  Проблематика В. л. развивалась уже по существу в древности (например, Аристотелем), а в новое время - Г. В. Лейбницем,Дж. Булем,У. С. Джевонсом,Дж. Венном.

 Как логическая система, В. л. - разновидность многозначной логики:истинным высказываниям (достоверным событиям) приписывается истинностное значение (вероятность) 1, ложным высказываниям (невозможным событиям) - значение 0; гипотетическим же высказываниям может приписываться в качестве значения любое действительное число из интервала (0, 1). Вероятность гипотезы, зависящая как от её содержания (формулировки), так и от информации об уже имеющемся знании («опыта»), есть их функция.Над истинностными значениями (вероятностями) гипотез определяются логические операции:конъюнкция (соответствующая умножению событий в теории вероятностей) и дизъюнкция (соответствующая сложению событий); мерой (значением) отрицания гипотезы является вероятность события, состоящего в её неподтверждении. Значения гипотез образуют при этом так называемую нормированную булеву алгебру, сравнительно простой и хорошо разработанный аппарат которой позволяет легко аксиоматизировать теорию вероятностей и является простейшим вариантом В. л.

  В соответствии с др. трактовкой понятия вероятности, связанной с так называемой частотной концепцией (определением) вероятности (А. Пуанкаре,М. Смолуховский,Р. Мизес ) ,в В. л. получили развитие идеи, согласно которым основным объектом её рассмотрения являются не вероятности отдельных событий, а случайные процессы,реализуемые в простейшем случае в виде случайных двоичных последовательностей, то есть последовательностей нулей и единиц (соответствующих единичным актам не наступления и наступления некоторого события при повторных испытаниях).

  Интенсивно развивается и проблематика В. л., возникающая при сопоставлении обоих упомянутых подходов (Р. Карнап,Б. Рассел и др.), а также базирующаяся на связи теоретико-вероятностных понятий с идеями теории информации и логической семантики. Все эти направления находятся в процессе разработки как по линии усовершенствования собственно математического аппарата В. л., так и в отношении теоретико-познавательной интерпретации возникающих систем (причём именно в последней области и сосредоточены главные трудности В. л.).

  Лит.см. при статьях Вероятностей теория, Индуктивная логика, Многозначная логика.

  Ю. А. Гастев.

Вероятностный автомат

Вероя'тностный автома'т,система, в которой переход из одного состояния в другое происходит случайным образом. Вероятность этого перехода определяется последовательностью его предыдущих состояний ( a ₁, a ₂,..., a _i,..., a _n) и входными сигналами ( S ₁, S ₂,..., S _m) и записывается в виде функции Р( a _i® a _j, S _k) ,где a _i® a _jозначает переход из состояния ( a _iв состояние a _j).

 В. а. используются в формальных моделях процессов обучения, в моделях сложного поведения, когда реакция автомата неоднозначна.

  Примером В. а. может служить система автоматического управления движением транспорта на перекрёстке двух улиц с разной интенсивностью движения. Для простоты рассмотрим В. а. с двумя состояниями: «откр» - проезд по магистрали (улица с интенсивным движением) открыт и «закр» - магистраль перекрыта, разрешено поперечное движение. Входных сигналов тоже два: S ₁- «на поперечной улице ждет транспорт» и S ₂-«эта улица пуста». Переходные вероятности определены так:

  Р(закр ® закр, S ₂) = Р(откр ® закр, S ₂) = 0;

  Р(откр ® откр, S ₂) = Р(закр ® откр, S ₂) = 1;

  Р(откр ® откр, S ₁) = 0,7;

  Р(откр ® закр, S ₁) = 0,3;

  Р(закр ® закр, S ₁) = 0,5;

  Р(закр ® откр, S ₁) =0,5.

  Такой автомат по мере надобности пропускает поперечный транспорт, но не перекрывает магистраль при появлении на поперечном направлении каждой отдельной машины. Численные значения вероятностей переходов и время основного такта работы автомата необходимо выбирать исходя из конкретного транспортного режима.

  В. а. можно представить в виде системы, состоящей из детерминированного автомата и случайных чисел датчика,подающего на один из входов автомата независимые сигналы с заданным распределением вероятностей.

  Ю. А. Шрейдер.

Вероятностный процесс

Вероя'тностный проце'сс,то же, что случайный процесс.

Вероятность

Вероя'тностьматематическая, числовая характеристика степени возможности появления какого-либо определённого события в тех или иных определённых, могущих повторяться неограниченное число раз условиях. Как категория научного познания понятие «В.» отражает особый тип связей между явлениями, характерных для массовых процессов. Категория В. лежит в основе особого класса закономерностей - вероятностных или статистических закономерностей.

  Численное значение В. в некоторых случаях получается из «классического» определения В.: В. равна отношению числа случаев, «благоприятствующих»- данному событию, к общему числу «равновозможных» случаев. Например, если из 10 млн. облигаций государственного выигрышного займа, на которые в одном тираже должен выпасть один выигрыш максимального размера, в данном городе размещено 500 тыс. облигаций, то В. того, что максимальный выигрыш достанется жителю данного города, равна 500000 / 10000000 = .

  В других, более сложных случаях определение численного значения В. требует статистического подхода. Например, если при 100 попытках стрелок попал в цель 39 раз, то можно думать, что для него В. попадания в цель при данных условиях приблизительно равна . По В., определённой классическим или статистическим способом, могут быть вычислены в соответствии с правилами теории вероятностей новые В. Например, если для нашего стрелка В. попадания при отдельном выстреле равна , то В. того, что он будет иметь хотя бы одно попадание при четырёх выстрелах, равна 1 - (1 - ) ⁴» 0 ,87. Этот вывод может быть проверен статистически: если попытки поразить цель хотя бы одним выстрелом из четырёх будут повторяться много раз, то они будут иметь успех приблизительно в 87% случаев (в. предположении, что за это время искусство стрелка не изменится заметным образом).

  Математическая В. является выражением качественно своеобразной связи между случайным и необходимым. При изложении теории вероятностей формулируются в виде аксиом те свойства В., которые на данном этапе развития науки необходимы для её развития. Однако ни эти аксиомы, ни классический подход к В., ни статистический подход не дают исчерпывающего определения реального содержания понятия «В.»; они являются лишь известными приближениями ко всё более полному его раскрытию. Далеко не всякое событие, наступление которого при заданных условиях не является однозначно определённым, имеет при этом комплексе условий определённую В. Предположение, что при данных условиях для данного события В., то есть вполне определённая нормальная доля числа появлений данного события при большом числе повторений данных условий, существует, является гипотезой, которая в каждом отдельном вопросе требует специальной проверки или обоснования. Например, имеет смысл говорить о В. попадания в цель заданных размеров, с заданного расстояния из винтовки известного образца стрелком, вызванным наудачу из определённого воинского подразделения. Однако было бы бессмысленно говорить о В. попадания в цель, если об условиях стрельбы ничего не известно.

  По поводу связи В. с частотой надо иметь в виду следующее: при конечном числе nповторений заданных условий доля числа случаев m,в которых данное событие появится, то есть так называемая частота m/n,как правило, мало отличается от вероятности р.Чем больше число повторений n,тем реже встречаются сколько-либо значительные отклонения частоты m/nот вероятности р.Для пояснения этого обстоятельства рассмотрим пример бросания монеты, в котором В. появления «герба» и «надписи» одинаковы и равны . При десяти бросаниях ( n =10) появление десяти «гербов» или десяти «надписей» очень мало вероятно. Но и утверждать, что «герб» выпадает ровно пять раз, нет достаточных оснований; более того, утверждая, что «герб» выпадает 4 или 5, или 6 раз, мы ещё довольно сильно рисковали бы ошибиться. Но при ста бросаниях монеты можно уже без практически ощутимого риска заранее утверждать, что число выпавших «гербов» будет лежать между 40 и 60 (см. подробнее Больших чисел закон ) .

 Математическая В. может служить для оценки В. события в обычном, житейском смысле, то есть для уточнения так называемых «проблематических» суждений, выражающихся обычно словами «возможно», «вероятно», «очень вероятно» и, т.п. По поводу этих оценок следует иметь в виду, что в применении к любому определённому суждению, которое на самом деле может быть только истинным или ложным, оценка его В. имеет лишь временный или же субъективный смысл, то есть выражает лишь наше отношение к делу. Например, если кто-либо, не имея по этому поводу специальных сведений, захочет представить себе вид окрестностей Москвы 23 марта 1930, то он скажет: «вероятно, в этот день на полях лежал снег». Однако на самом деле в 1930 снег под Москвой к 22 марта уже сошёл с полей. Выяснив это обстоятельство, мы должны будем отменить первоначальную оценку, выраженную заключённым в кавычки проблематичным суждением. Тем не менее эта оценка, оказавшаяся в применении к данному индивидуальному случаю ошибочной, основана на верном общем правиле: «в начале двадцатых чисел марта на полях под Москвой по большей части лежит снег». Это правило отражает объективные свойства климата Подмосковья. Такого рода правила можно выражать, указывая уровень В. интересующего нас события, при тех или иных общих, осуществимых неограниченное число раз условиях. Эти оценки уже имеют объективный смысл. Поэтому употребление расчёта В. для подтверждения наших оценок степени надёжности тех или иных утверждений, относящихся к отдельным индивидуальным событиям, не должно давать повода к мнению, что математическая В. является только числовым выражением нашей субъективной уверенности в наступлении некоторого события. Такое идеалистическое, субъективное понимание смысла математической В. является ошибочным. При последовательном развитии оно приводит к абсурдному утверждению, что из чистого незнания, анализируя одни лишь субъективные состояния нашей большей или меньшей уверенности, мы можем сделать какие-либо определённые заключения относительно внешнего мира.

  Описанное выше употребление расчёта В. для оценки положения в отдельных индивидуальных случаях неизбежно приводит к вопросу о том, какими В. можно пренебрегать на практике. Этот вопрос решается по-разному, в зависимости от того, насколько велика необходимость быстрого перехода от накопления надёжных данных к их действенному употреблению. Например, если при данных условиях стрельбы теоретический расчёт приводит к тому, что поставленная боевая задача будет решена данным числом выстрелов с В. 0,95 (то есть В. того, что назначенного числа снарядов не хватит, равна 0,05), то обычно считают возможным исходить при руководстве боевыми операциями из предположения, что назначенное число снарядов окажется достаточным. В более спокойной обстановке научных исследований принято пренебрегать лишь В. в 0,003 (эта норма связана с так называемым правилом трёх сигма), а иногда требовать и ещё большего приближения В. отсутствия ошибки к единице. В математической статистике В., которой решено пренебрегать в данном исследовании, называется значимости уровнем.Хотя в статистике обычно рекомендуют пользоваться уровнями значимости от 0,05 при предварительных ориентировочных исследованиях до 0,001 при окончательных серьёзных выводах, часто достижима значительно большая достоверность вероятностных выводов. Например, основные выводы статистической физики основаны на пренебрежении лишь В. порядка меньшего 0,0000000001.

  Подробнее об употреблении вероятностных методов в науке см. в статьях Вероятностей теория и Математическая статистика.

  Лит.:Математика, её содержание, методы и значение, т. 2, М., 1956, гл. 11; Колмогоров А. Н., К логическим основам теории информации и теории вероятностей, в сборнике: Проблемы передачи информации, т. 5, в. 3, М., 1969.

  А. Н. Колмогоров.

Вероятность безотказной работы

Вероя'тность безотка'зной рабо'ты,показатель надёжности устройства, схемы или отдельного элемента, который оценивает возможность сохранения изделием работоспособности в определённом интервале времени или при выполнении заданного объёма работы.

Вероятность перехода

Вероя'тность перехо'дав квантовой механике, см. Квантовые переходы.

Вероятность термодинамическая

Вероя'тность термодинами'ческая,число способов, которыми может быть реализовано состояние физической системы. В термодинамике состояние физической системы характеризуется определёнными значениями плотности, давления, температуры и др. измеримых величин. Перечисленные величины определяют состояние системы в целом (её макросостояние). Однако при одной и той же плотности, температуре и т.д. частицы системы могут различными способами распределиться в пространстве и иметь различные импульсы. Каждое данное распределение частиц называется микросостоянием системы. В. т. (обозначается W) равна числу микросостояний, реализующих данное макросостояние, из чего следует, что W³ 1. В. т. связана с одной из основных макроскопических характеристик системы энтропией Sсоотношением Больцмана: S= klnW, где k - Больцмана постоянная.